题目内容
1.在同一坐标系中,一次函数y=ax+c与二次函数y=ax2+(a+c)x+c的图象可能是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据二次函数的开口方向,与y轴的交点;一次函数经过的象限,与y轴的交点可得相关图象.
解答 解:A、y=ax2+(a+c)x+c=(ax+c)(x+1),故此二次函数与x轴的两个交点为(-$\frac{c}{a}$,0),(-1,0),一次函数y=ax+c与x轴的交点为(-$\frac{c}{a}$,0),故两函数在x轴上有交点,正确;
B、一次函数y=ax+c的图象过一、三象限,a>0,与二次函数开口向下,即a<0相矛盾,错误;
C、一次函数y=ax+c的图象过二、四象限,a<0,与二次函数开口向上,a>0相矛盾,错误;
D、两个函数在x轴上没有交点,错误.
故选:A.
点评 此题考查二次函数及一次函数的图象的性质;用到的知识点为:二次函数和一次函数的常数项是图象与y轴交点的纵坐标;一次函数的一次项系数大于0,图象经过一、三象限;小于0,经过二、四象限;二次函数的二次项系数大于0,图象开口向上;二次项系数小于0,图象开口向下

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | $\sqrt{4}$-$\sqrt{3}$=1 | B. | $\sqrt{2}$×$\sqrt{\frac{1}{2}}$=1 | C. | $\sqrt{6}$÷$\sqrt{2}$=2 | D. | $\sqrt{8}$=±2$\sqrt{2}$ |
12.下面命题中,假命题是( )
| A. | 有一个角是100°的两个等腰三角形相似 | |
| B. | 全等三角形都是相似三角形 | |
| C. | 两边对应成比例,且有一个角相等的两个三角形相似 | |
| D. | 两条直角边对应成比例的两个直角三角形相似 |
9.对于下列各式,其中错误的是( )
| A. | -15<0 | B. | 2.9>-3.1 | C. | -10>-9 | D. | |0.23|>-|0.32| |
16.下面四个图形中,∠1与∠2是对顶角的图形的个数是( )


| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
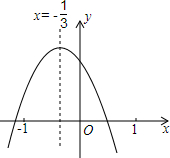 小明从如图所示的二次函数y=ax2+bx+c(a≠0)图象中,观察得出了下面四条信息:①a=$\frac{3}{2}$b;②b2-4ac=0;③ab>0;④a+b+c<0;
小明从如图所示的二次函数y=ax2+bx+c(a≠0)图象中,观察得出了下面四条信息:①a=$\frac{3}{2}$b;②b2-4ac=0;③ab>0;④a+b+c<0; 如图所示,M是AC的中点,N是BC的中点,若AM=1cm,BN=1.5cm.求AB的长.
如图所示,M是AC的中点,N是BC的中点,若AM=1cm,BN=1.5cm.求AB的长. OA是表示北偏东30°方向的一条射线,仿照这条射线画出表示下列方向的射线:
OA是表示北偏东30°方向的一条射线,仿照这条射线画出表示下列方向的射线: