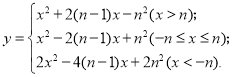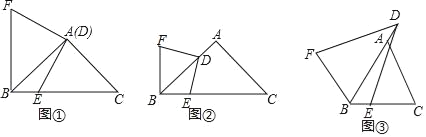
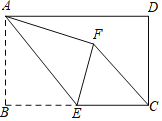
[题目]如图.在矩形ABCD中.AB＝4.BC＝6.点E为BC的中点.将△ABE沿AE折叠.使点B落在矩形内的点F处.连接CF.则CF的长为()A.B.C.D. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在矩形ABCD中，AB＝4，BC＝6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内的点F处，连接CF，则CF的长为（）

A.B.C.D.

【答案】C

【解析】

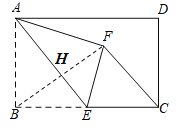
连接BF，（见详解图），由翻折变换可知，BF⊥AE，BE=EF，由点E是BC的中点，可知BE=3，根据勾股定理即可求得AE；根据三角形的面积公式可求得BH，进而可得到BF的长度；结合题意可知FE=BE=EC，进而可得∠BFC=90°，至此，在Rt△BFC中，利用勾股定理求出CF的长度即可

如图，连接BF．

∵△AEF是由△ABE沿AE折叠得到的，

∴BF⊥AE，BE=EF．

∵BC=6，点E为BC的中点，

∴BE=EC=EF=3

根据勾股定理有AE=AB+BE

代入数据求得AE=5

根据三角形的面积公式

得BH=

即可得BF=

由FE=BE=EC，

可得∠BFC=90°

再由勾股定理有BC-BF=CF

代入数据求得CF=

故答案为：

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

【题目】第二十四届冬季奧林匹克运动会将于2022年2月4日至2月20日在北京举行，北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛，甲、乙两校各有名学生参加活动，为了解这两所学校的成绩情况，进行了抽样调查，过程如下，请补充完整.

[收集数据]

从甲、乙两校各随机抽取名学生，在这次竞赛中他们的成绩如下:

甲：

乙：

[整理、描述数据]按如下分数段整理、描述这两组样本数据:

学校

人数

成绩

甲

乙

(说明:优秀成绩为，良好成绩为合格成绩为.)

[分析数据]两组样本数据的平均分、中位数、众数如下表所示:

学校	平均分	中位数	众数
甲
乙

其中 .

[得出结论]

（1）小明同学说:“这次竞赛我得了分，在我们学校排名属中游略偏上!”由表中数据可知小明是 _校的学生；(填“甲”或“乙”)

（2）张老师从乙校随机抽取--名学生的竞赛成绩，试估计这名学生的竞赛成绩为优秀的概率为_ ；

（3）根据以上数据推断一所你认为竞赛成绩较好的学校，并说明理由: ；

(至少从两个不同的角度说明推断的合理性)

【题目】在中，，点为直线上一动点（点不与点重合），以为腰作等腰直角，使，连接．

（1）观察猜想

如图1，当点在线段上时，

①与的位置关系为__________；

②之间的数量关系为___________（提示：可证）

（2）数学思考

如图2，当点在线段的延长线上时，（1）中的①、②结论是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明；

（3）拓展延伸

如图3，当点在线段的延长线时，将沿线段翻折，使点与点重合，连接，若，请直接写出线段的长．（提示：做于，做于）

【题目】如图，A是上一动点，D是弦BC上一定点，连接AB，AC，AD．设线段AB的长是xcm，线段AC的长是cm，线段AD的长是cm．

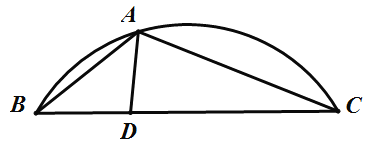
小腾根据学习函数的经验，分别对函数，随自变量x的变化的关系进行了探究．下面是小腾的探究过程，请补充完整：

（1）对于点A在上的不同位置，画图、测量，得到了，的长度与x的几组值：

	位置1	位置2	位置3	位置4	位置5	位置6	位置7	位置8
x/cm	0.00	0.99	2.01	3.46	4.98	5.84	7.07	8.00
/cm	8.00	7.46	6.81	5.69	4.26	3.29	1.62	0.00
/cm	2.50	2.08	1.88	2.15	2.99	3.61	4.62	m

请直接写出上表中的m值是；

（2）在同一平面直角坐标系中，描出补全后表中各组数据所对应的点(x，)，(x，)，并画出函数，的图象；

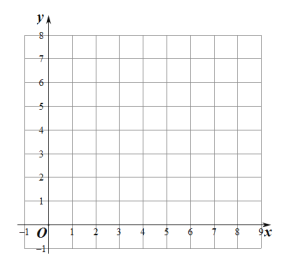
（3）结合函数图象，解决问题：当AC=AD时，AB的长度约为 cm；当AC=2AD时，AB的长度约为 cm．

【题目】在一个不透明的袋子中，装有除颜色外其余均相同的红、蓝两种球，已知其中红球有3个，且从中任意摸出一个是红球的概率为0.75.

（1）根据题意，袋中有个蓝球.

（2）若第一次随机摸出一球，不放回，再随机摸出第二个球.请用画树状图或列表法求“摸到两球中至少一个球为蓝球（记为事件A）”的概率P（A）.

【题目】在平面直角坐标系中，点A是y轴上一点，其坐标为（0，6），点B在x轴的正半轴上．点P，Q均在线段AB上，点P的横坐标为m，点Q的横坐标大于m，在△PQM中，若PM∥x轴，QM∥y轴，则称△PQM为点P，Q的“肩三角形．

（1）若点B坐标为（4，0），且m＝2，则点P，B的“肩三角形”的面积为　　；

（2）当点P，Q的“肩三角形”是等腰三角形时，求点B的坐标；

（3）在（2）的条件下，作过O，P，B三点的抛物线y＝ax2+bx+c

①若M点必为抛物线上一点，求点P，Q的“肩三角形”面积S与m之间的函数关系式，并写出自变量m的取值范围．

②当点P，Q的“肩三角形”面积为3，且抛物线y＝ax2+bx+c与点P，Q的“肩三角形”恰有两个交点时，直接写出m的取值范围．

【题目】观察猜想：（1）如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC＝3，点D与点A重合，点E在边BC上，连接DE，将线段DE绕点D顺时针旋转90°得到线段DF，连接BF，BE与BF的位置关系是　　，BE+BF＝　　；

探究证明：（2）在（1）中，如果将点D沿AB方向移动，使AD＝1，其余条件不变，如图②，判断BE与BF的位置关系，并求BE+BF的值，请写出你的理由或计算过程；

拓展延伸：（3）如图③，在△ABC中，AB＝AC，∠BAC＝a，点D在边BA的延长线上，BD＝n，连接DE，将线段DE绕着点D顺时针旋转，旋转角∠EDF＝a，连接BF，则BE+BF的值是多少？请用含有n，a的式子直接写出结论．

【题目】已知函数其中是常数，且＞0．

（1）若点（，2）在函数的图象上，求的值．

（2）当=1时，①当≤≤2时，求函数值的取值范围．

②当≤≤时，函数图象上的点到轴的距离恒（永远）小于6，求的取值范围．

（3）直接写出函数图象与有两个交点时的取值范围．

【题目】为切实加强中小学生交通安全宣传教育，让学生真正知危险、会避险，郑州市某中学开展了“交通安全进校园”系列活动．为了解七、八年级学生对交通安全知识的掌握情况，对七、八年级学生进行了测试，现从两年级中各随机抽取20名学生的测试成绩（百分制）进行整理、描述和分析（成绩不低于90分为优秀）．

测试成绩（百分制）如下：

七年级：52，78，82，86，77，83，92，87，72，81，93，98，81，69，87，86，80，81，82，94

八年级：87，77，90，79，93，83，88，84，82，94，86，88，57，68，89，59，81，90，88，95

分组整理，描述数据

分组	七年级		八年级
分组	画“正”计数	频数	画“正”计数	频数
	一	1		2
	一	1	一	1
				2
			正正	10
		4	正	5

七、八年级抽取学生的测试成绩统计表

年级	平均数	中位数	众数	优秀率
七年级	82		81	20%
八年级	82.5	86.5		25%

根据以上信息，回答下列问题：

（1）表中__________，__________，__________，；

（2）若该校七年级270人和八年级280人参加了此次测试，估计参加此次测试成绩优秀的学生人数；

（3）根据以上数据，你认为该校七、八年级哪个年级学生掌握交通安全知识较好？并说明理由？

试题分类