题目内容
已知关于x的方程x2-(2k+1)x+k2+2=0的两个实数根的平方和等于13,求k的值.
考点:根与系数的关系,根的判别式
专题:计算题
分析:设方程的两个实数根分别为a,b,先根据根的判别式确定k的取值范围为k≥
,再根据根与系数的关系得a+b=2k+1,ab=k2+2,接着利用a2+b2=13得到(2k+1)2-2(k2+2)=13,整理得k2+2k-8=0,解得k1=-4,k2=2,然后根据k的范围确定k的值.
| 7 |
| 4 |
解答:解:设方程的两个实数根分别为a,b,
△=(2k+1)2-4(k2+2)≥0,解得k≥
,
根据根与系数的关系得a+b=2k+1,ab=k2+2,
∵a2+b2=13,
∴(a+b)2-2ab=13,
∴(2k+1)2-2(k2+2)=13,
整理得k2+2k-8=0,解得k1=-4,k2=2,
∴k的值为2.
△=(2k+1)2-4(k2+2)≥0,解得k≥
| 7 |
| 4 |
根据根与系数的关系得a+b=2k+1,ab=k2+2,
∵a2+b2=13,
∴(a+b)2-2ab=13,
∴(2k+1)2-2(k2+2)=13,
整理得k2+2k-8=0,解得k1=-4,k2=2,
∴k的值为2.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
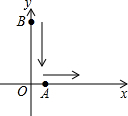 如图,两条直线互相垂直于点O,点A位于O处,以2cm/s的速度向右匀速移动,点B位于O的正上方18cm处,以3cm/s的速度与A同时开始向下匀速移动,多长时间时△AOB的面积为24cm2?
如图,两条直线互相垂直于点O,点A位于O处,以2cm/s的速度向右匀速移动,点B位于O的正上方18cm处,以3cm/s的速度与A同时开始向下匀速移动,多长时间时△AOB的面积为24cm2?