题目内容
 如图,在Rt△OAB中,∠A=90°,∠ABO=30°,OB=
如图,在Rt△OAB中,∠A=90°,∠ABO=30°,OB= ,边AB的垂直平分线CD分别与AB、x轴、y轴交于点C、G、D.
,边AB的垂直平分线CD分别与AB、x轴、y轴交于点C、G、D.
(1)求点G的坐标;
(2)求直线CD的解析式;
(3)在直线CD上和平面内是否分别存在点Q、P,使得以O、D、P、Q为顶点的四边形是菱形?若存在,求出点Q得坐标;若不存在,请说明理由.
解:(1)∵DC是AB垂直平分线,OA垂直AB,
∴G点为OB的中点,
∵OB= ,
,
∴G(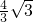 ,0).
,0).
(2)过点C作CH⊥x轴于点H,
在Rt△ABO中,∠ABO=30°,OB= ,
,
∴cos30°= =
= ,
,
即AB= ×
× =4,
=4,
又∵CD垂直平分AB,
∴BC=2,在Rt△CBH中,CH= BC=1,BH=
BC=1,BH= ,
,
∴OH= -
- =
=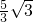 ,
,
∴C(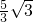 ,-1),
,-1),
∵∠DGO=60°,
∴OG= OB=
OB=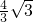 ,
,
∴OD=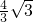 tan60°=4,
tan60°=4,
∴D(0,4),
设直线CD的解析式为:y=kx+b,则 ,解得:
,解得:
∴y=- x+4;
x+4;
(3)存在点Q、P,使得以O、D、P、Q为顶点的四边形是菱形.
①如图,当OD=DQ=QP=OP=4时,四边形DOPQ为菱形,

设QP交x轴于点E,在Rt△OEP中,OP=4,∠OPE=30°,
∴OE=2,PE=2 ,
,
∴Q(2,4-2 ).
).
②如图,当OD=DQ=QP=OP=4时,四边形DOPQ为菱形,
延长QP交x轴于点F,在Rt△POF中,OP=4,∠FPO=30°,
∴OF=2,PF=2 ,
,
∴QF=4+2
∴Q(-2,4+2 ).
).

③如图,当PD=DQ=QO=OP=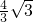 时,四边形DOPQ为菱形,在Rt△DQM中,∠MDQ=30°,
时,四边形DOPQ为菱形,在Rt△DQM中,∠MDQ=30°,
∴MQ= DQ=
DQ=
∴Q( ,2).
,2).

④如图,当OD=OQ=QP=DP=4时,四边形DOQP为菱形,
设PQ交x轴于点N,此时∠NOQ=∠ODQ=30°,
在Rt△ONQ中,NQ= OQ=2,
OQ=2,

∴ON=2 ,
,
∴Q(2 ,-2);
,-2);
综上所述,满足条件的点Q共有四点:(2,4-2 ),(-2,4+2
),(-2,4+2 ),(
),( ,2),(2
,2),(2 ,-2);
,-2);
分析:(1)根据DC是AB垂直平分线,得出G点为OB的中点,再根据OB的值,即可求出点G的坐标;
(2)先过点C作CH⊥x轴,在Rt△ABO中,根据∠ABO的度数和OB的值求出AB的长,再在Rt△CBH中,求出OH的值,得出点D的坐标,再设直线CD的解析式,得出k,b的值,即可求出直线CD的解析式;
(3)首先判断出存在点Q、P,使得以O、D、P、Q为顶点的四边形是菱形,再分四种情况进行讨论,根据条件画出图形,分别根据Q点的不同位置求出Q的坐标即可.
点评:此题考查了一次函数的综合应用;解题的关键是对(3)中Q点的不同位置分别进行求解,不要漏掉.
∴G点为OB的中点,
∵OB=
 ,
,∴G(
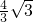 ,0).
,0).(2)过点C作CH⊥x轴于点H,
在Rt△ABO中,∠ABO=30°,OB=
 ,
,∴cos30°=
 =
= ,
,
即AB=
 ×
× =4,
=4,又∵CD垂直平分AB,
∴BC=2,在Rt△CBH中,CH=
 BC=1,BH=
BC=1,BH= ,
,∴OH=
 -
- =
=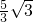 ,
,∴C(
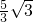 ,-1),
,-1),∵∠DGO=60°,
∴OG=
 OB=
OB=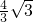 ,
,∴OD=
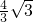 tan60°=4,
tan60°=4,∴D(0,4),
设直线CD的解析式为:y=kx+b,则
 ,解得:
,解得:
∴y=-
 x+4;
x+4;(3)存在点Q、P,使得以O、D、P、Q为顶点的四边形是菱形.
①如图,当OD=DQ=QP=OP=4时,四边形DOPQ为菱形,

设QP交x轴于点E,在Rt△OEP中,OP=4,∠OPE=30°,
∴OE=2,PE=2
 ,
,∴Q(2,4-2
 ).
).②如图,当OD=DQ=QP=OP=4时,四边形DOPQ为菱形,
延长QP交x轴于点F,在Rt△POF中,OP=4,∠FPO=30°,
∴OF=2,PF=2
 ,
,∴QF=4+2

∴Q(-2,4+2
 ).
).
③如图,当PD=DQ=QO=OP=
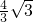 时,四边形DOPQ为菱形,在Rt△DQM中,∠MDQ=30°,
时,四边形DOPQ为菱形,在Rt△DQM中,∠MDQ=30°,∴MQ=
 DQ=
DQ=
∴Q(
 ,2).
,2).
④如图,当OD=OQ=QP=DP=4时,四边形DOQP为菱形,
设PQ交x轴于点N,此时∠NOQ=∠ODQ=30°,
在Rt△ONQ中,NQ=
 OQ=2,
OQ=2,
∴ON=2
 ,
,∴Q(2
 ,-2);
,-2);综上所述,满足条件的点Q共有四点:(2,4-2
 ),(-2,4+2
),(-2,4+2 ),(
),( ,2),(2
,2),(2 ,-2);
,-2);分析:(1)根据DC是AB垂直平分线,得出G点为OB的中点,再根据OB的值,即可求出点G的坐标;
(2)先过点C作CH⊥x轴,在Rt△ABO中,根据∠ABO的度数和OB的值求出AB的长,再在Rt△CBH中,求出OH的值,得出点D的坐标,再设直线CD的解析式,得出k,b的值,即可求出直线CD的解析式;
(3)首先判断出存在点Q、P,使得以O、D、P、Q为顶点的四边形是菱形,再分四种情况进行讨论,根据条件画出图形,分别根据Q点的不同位置求出Q的坐标即可.
点评:此题考查了一次函数的综合应用;解题的关键是对(3)中Q点的不同位置分别进行求解,不要漏掉.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
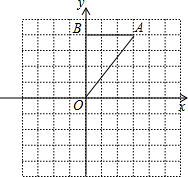 如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).
如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).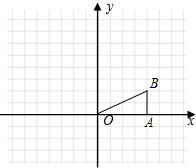 OA1B1.
OA1B1.
 如图,在Rt△OAB中,∠OBA=90°,OB=AB=4,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
如图,在Rt△OAB中,∠OBA=90°,OB=AB=4,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1. (2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.