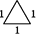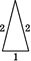题目内容

已知：x2+xy+y=14，y2+xy+x=28，求x+y的值．

-7或6 【解析】试题分析：由x2+xy+y=14，y2+xy+x=28，即可求得x2+2xy+y2+x+y=42，则变形得（x+y）2+（x+y）-42=0，将x+y看作整体，利用因式分解法即可求得x+y的值． 试题解析： ∵x2+xy+y=14①，y2+xy+x=28②， ∴①+②，得：x2+2xy+y2+x+y=42， ∴（x+y）2+（x+y）-42=0， ...
练习册系列答案
相关题目

如图，在△ABC和△DEF中，∠B=∠DEF，AB=DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（　 　）

A. ∠A=∠D B. BC=EF C. ∠ACB=∠F D. AC=DF

D 【解析】【解析】 ∵∠B=∠DEF，AB=DE，∴添加∠A=∠D，利用ASA可得△ABC≌△DEF； ∴添加BC=EF，利用SAS可得△ABC≌△DEF； ∴添加∠ACB=∠F，利用AAS可得△ABC≌△DEF； 故选D．

根据下列条件,判断△ABC的形状.

(1)∠A=40°,∠B=80°;

(2)∠A∶∠B∶∠C=2∶3∶7.

(1)△ABC是锐角三角形(2)△ABC是钝角三角形. 【解析】试题分析：（1）根据三角形的内角和是180°求出∠C的度数即可判断△ABC的形状； （2）因为∠A∶∠B∶∠C＝2∶3∶7，所以可设∠A＝2x，∠B＝3x，∠C＝7x，根据三角形内角和是180°列出方程求出∠A、∠B、∠C的度数，即可判断△ABC的度数． 试题解析： （1）∠C＝180°－∠A－∠B＝60°,因...

如图,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的哪个性质?

答:______.

稳定性 【解析】塔吊的上部是三角形结构，可以保证安全吊塔上部的结构的稳定性，应用了三角形的稳定性，故答案为：三角形的稳定性

满足下列条件的两个三角形不一定全等的是(　 　)

A. 有一边相等的两个等边三角形

B. 有一腰和底边对应相等的两个等腰三角形

C. 周长相等的两个三角形

D. 斜边和一条直角边对应相等的两个等腰直角三角形

C 【解析】A.根据全等三角形的判定，可知有一边相等的两个等边三角形全等，故选项A不符合； B.根据全等三角形的判定，可知有一腰和底边对应相等的两个等腰三角形全等，故选项B不符合； C.根据全等三角形的判定，可知周长相等的两个三角形不一定全等，故选项C符合； D.根据全等三角形的判定，可知斜边和直角边对应相等的两个等腰直角三角形全等，故选项B不符合. 故本题应选C. ...

若x2-y2=48，x+y=6，则3x-3y=_____．

24 【解析】∵x2-y2=（x+y）（x-y）=48，x+y=6， ∴x-y=8， ∴3x-3y=3（x-y）=24.

计算(a+1)2(a-1)2的结果是( )

A. a4-1 B. a4+1 C. a4+2a2+1 D. a4-2a2+1

D 【解析】原式=，故选D.

按如图方式摆放餐桌和椅子．用x来表示餐桌的张数，用y来表示可坐人数．

①题中有几个变量？

②你能写出两个变量之间的关系吗？

①有2个变量；②能，函数关系式可以为y=4x+2． 【解析】试题分析：①根据变量和常量的定义可得结果； ②由图形可知，第一张餐桌上可以摆放6把椅子，进一步观察发现：多一张餐桌，多放4把椅子．x张餐桌共有6+4（x﹣1）=4x+2． 试题解析：①观察图形：x=1时，y=6，x=2时，y=10；x=3时，y=14；… 可见每增加一张桌子，便增加4个座位， 因此x张餐桌共有...

在平面内,分别用3根、5根、6根……火柴棒首尾依次相接,能搭成什么形状的三角形呢?通过尝试,列表如下.

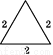
火柴棒数

3

5

6

…

示意图

…

形状

等边三角形

等腰三角形

等边三角形

…

问:(1)4根火柴棒能搭成三角形吗?

(2)8根、12根火柴棒分别能搭成几种不同形状的三角形?并画出它们的示意图.

(1)4根火柴棒不能搭成三角形(2)8根火柴棒能搭成一种三角形,12根火柴棒能搭成三种不同的三角形:(4,4,4),(5,5,2),(3,4,5) 【解析】试题分析： （1）由“三角形三边间的关系”可知，四根火柴棒不能围成三角形； （2）结合“三角形三边间的关系”分析可知：①8根火柴棒能搭成一种三角形，其边长分别为2、3、3，再根据边长画出示意图即可；②12根火柴棒可以搭成三种三...

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网