题目内容
4.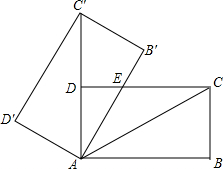 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为$\sqrt{3}$.
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为$\sqrt{3}$.
分析 先求出∠ACD=30°,进而可算出CE、AD,再算出△AEC的面积.
解答 解:如图,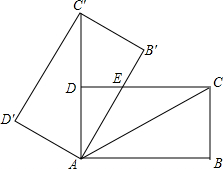
由旋转的性质可知:AC=AC',
∵D为AC'的中点,
∴AD=$\frac{1}{2}AC'=\frac{1}{2}AC$,
∵ABCD是矩形,
∴AD⊥CD,
∴∠ACD=30°,
∵AB∥CD,
∴∠CAB=30°,
∴∠C'AB'=∠CAB=30°,
∴∠EAC=30°,
∴AE=EC,
∴DE=$\frac{1}{2}AE=\frac{1}{2}EC$,
∴CE=$\frac{2}{3}CD$=$\frac{2}{3}AB=2$,
DE=$\frac{1}{3}AB=1$,
AD=$\sqrt{3}$,
∴${S}_{△AEC}=\frac{1}{2}×EC×AD$=$\sqrt{3}$.
故答案为$\sqrt{3}$.
点评 本题考查了旋转的性质、矩形的性质、特殊角的三角函数,三角形面积计算等知识点,难度不大.清楚旋转的“不变”特性是解答的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
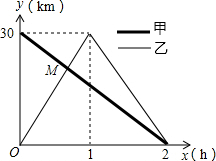 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A第,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A第,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: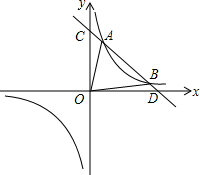 如图,已知一次函数y1=-x+a与x轴、y轴分别交于点D、C两点和反比例函数y2=$\frac{k}{x}$交于A、B两点,且点A的坐标是(1,3),点B的坐标是(3,m).
如图,已知一次函数y1=-x+a与x轴、y轴分别交于点D、C两点和反比例函数y2=$\frac{k}{x}$交于A、B两点,且点A的坐标是(1,3),点B的坐标是(3,m).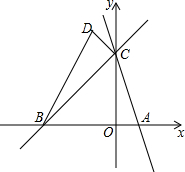 如图:直线y=-3x+3与x轴交于点A,与y轴交于点C,直线BC与x轴交于B(-3,0),与y轴交于点C.
如图:直线y=-3x+3与x轴交于点A,与y轴交于点C,直线BC与x轴交于B(-3,0),与y轴交于点C. 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为6,sinB=$\frac{1}{2}$,则线段AC的长是6.
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为6,sinB=$\frac{1}{2}$,则线段AC的长是6.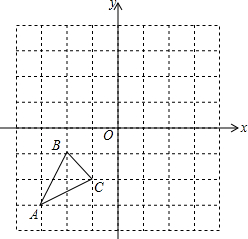 如图,在单位长度为1的方格中,若以点O为坐标原点建立平面直角坐标系,A(-3,-3),B(-2,-1),C(-1,-2).
如图,在单位长度为1的方格中,若以点O为坐标原点建立平面直角坐标系,A(-3,-3),B(-2,-1),C(-1,-2).