Question

已知：a、b、c为实数，且多项式x³＋ax²＋bx＋c能够被x²＋3x－4整除．

（1）求4a＋c的值．

（2）求2a－2b－c的值．

（3）若a、b、c为整数，且c≥a＞1，试确定a、b、c的大小．

Answer 1

(1)  ∵ x²＋3x－4＝(x－1)(x＋4)，

∴  x－1，x＋4都能整除x³＋ax²＋bx＋c，

∵  (x－1)｜x³＋ax²＋bx＋c，

∴  1＋a＋b＋c＝0，

∵  (x＋4)｜x³＋ax²＋bx＋c，

∴  －64＋16a－4b＋c＝0，

4×①＋②得   20a＋5c＝60，

∴       4a＋c＝12．    ③

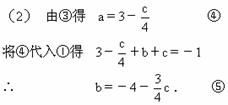
将④、⑤代入2a－2b－c中，得

∴  1＜a＜3，由a为整数知a＝2，

当a＝2时，代入③得c＝4，

再一起代入①，得b＝－7．