题目内容
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,两等圆⊙A、⊙B外切,那么图中阴影部分的面积为
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,两等圆⊙A、⊙B外切,那么图中阴影部分的面积为考点:相切两圆的性质,扇形面积的计算
专题:
分析:已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,则根据勾股定理可知AB=5,两个扇形的面积的圆心角之和为90度,利用扇形面积公式即可求解.
解答:解:∵Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB=
=5,
∴S空白部分=
=
,
∴图中阴影部分的面积为:S△ACB-S空白部分=
×3×4-
=6-
.
故答案为:6-
.
∴AB=
| 42+32 |
∴S空白部分=
90π×(
| ||
| 360 |
| 25π |
| 16 |
∴图中阴影部分的面积为:S△ACB-S空白部分=
| 1 |
| 2 |
| 25π |
| 16 |
| 25π |
| 16 |
故答案为:6-
| 25π |
| 16 |
点评:本题主要考查勾股定理的使用及扇形面积公式的灵活运用,得出空白面积是解题关键.

练习册系列答案
相关题目
一个三角形的三边的比为5:12:13.它的周长为60cm,则它的面积是( )
| A、100 | B、110 |
| C、120 | D、150 |
 将一个有45°角的三角板的直角顶点C放在一张宽为5cm的纸带边沿上.另一个顶点B在纸带的另一边沿上,测得∠DBC=30°,则三角板的最大边的长为
将一个有45°角的三角板的直角顶点C放在一张宽为5cm的纸带边沿上.另一个顶点B在纸带的另一边沿上,测得∠DBC=30°,则三角板的最大边的长为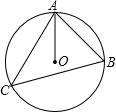 如图,⊙O是△ABC的外接圆,已知∠B=58°,则∠CAO的度数是
如图,⊙O是△ABC的外接圆,已知∠B=58°,则∠CAO的度数是 如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于
如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于