题目内容
20．已知k是不大于10的正整数，试找出一个k的值，使关于x的方程5x-6k=$\frac{1}{2}$（x-5k-1）的解也是正整数，并求出此时方程的解．分析 根据题意可以用含k的代数式表示出x，然后根据k是不大于10的正整数，关于x的方程5x-6k=$\frac{1}{2}$（x-5k-1）的解也是正整数可以得到k的值和x的值．
解答 解：∵5x-6k=$\frac{1}{2}$（x-5k-1）
解得，x=$\frac{7k-1}{9}$，
∵k是不大于10的正整数，关于x的方程5x-6k=$\frac{1}{2}$（x-5k-1）的解也是正整数，
∴k=4，x=3，
即此方程的解是x=3．
点评 本题考查解一元一次方程，解答本题的关键是明确解一元一次方程的方法，利用题目中条件，求出相应的k和x的值．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
8．△ABC中，直线DE交AB于点D，交AC于点E，以下能推出DE∥BC的条件是（ ）
| A． | $\frac{AD}{AB}$=$\frac{3}{4}$，$\frac{AE}{EC}$=$\frac{3}{4}$ | B． | $\frac{AD}{AB}$=$\frac{3}{4}$，$\frac{DE}{BC}$=$\frac{3}{4}$ | C． | $\frac{AD}{DB}$=$\frac{2}{3}$，$\frac{CE}{EA}$=$\frac{2}{3}$ | D． | $\frac{AB}{AD}$=$\frac{4}{3}$，$\frac{EC}{AE}$=$\frac{1}{3}$ |
5．下列运算中能用平方差公式的是（ ）
| A． | （3x+9）（9x+3） | B． | （2n+5）（n-3） | C． | （2-x）（2+x） | D． | （2+x）（2+x） |
9．
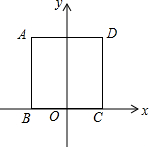正方形ABCD在直角坐标系中如图放置，B点的坐标是（-2，0），C点的坐标是（2，0），则A点的坐标是（ ）
正方形ABCD在直角坐标系中如图放置，B点的坐标是（-2，0），C点的坐标是（2，0），则A点的坐标是（ ）| A． | （4，-2） | B． | （-2，1） | C． | （2，4） | D． | （-2，4） |
10．下列各式变形正确的是（ ）
| A． | $\frac{2}{2+a}=\frac{1}{1+a}$ | B． | $\frac{1}{x+1}=\frac{x-1}{{{x^2}-1}}$ | C． | $\frac{-x+y}{x-y}=\frac{x+y}{y-x}$ | D． | $\frac{{{a^2}-1}}{a+1}=a-1$ |