Question

【题目】如图，在中，，点在边上，于点．

若，，求的长；

设点在线段上，点在射线上，以，，为顶点的三角形与有一个锐角相等，交于点．问：线段可能是的高线还是中线？或两者都有可能？请说明理由．

Answer 1

【答案】（1）6；（2）见解析

【解析】

（1）根据已知条件易证DE∥BC，再由平行线分线段成比例定理列比例式即可求解；（2）分三种情况讨论：①若∠CFG=∠ECD，此时线段CP是△CFG的FG边上的中线；②若∠CFG=∠EDC，此时线段CP为△CFG的FG边上的高线；③当CD为∠ACB的平分线时，CP既是△CFG的FG边上的高线又是中线．

解：∵，，

∴，

∴，

∵，，

∴；

①如图，若，此时线段是的边上的中线．

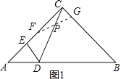
证明：∵，，

又∵，

∴，

∴，

∵，

∴，

∴，

∴线段是的边上的中线；

②如图，若，此时线段为的边上的高线．

证明：∵，

∴，

∵，

∴，

∴，

∴线段为的边上的高线．

③如图，当为的平分线时，既是的边上的高线又是中线．