题目内容
 如图,A是双曲线y=
如图,A是双曲线y=| 8 |
| x |
| 2 |
| x |
分析:设出A的坐标为(a,b)(a>0,b>0),表示出AE与AF,将A的坐标代入y=
(x>0)中求出ab的值,而矩形AEOF的面积等于AE与AF的乘积,即为ab的值,确定出矩形AEOF的面积,设出C和B的坐标,同理求出三角形OCF与三角形BOE的面积,用矩形AEOF的面积-三角形OCF的面积-三角形BOE的面积,即可得到四边形ABOC的面积.
| 8 |
| x |
解答:解:设A(a,b)(a>0,b>0),则AE=b,AF=a,
将x=a,y=b代入反比例函数y=
得:ab=8,
∴S矩形AEOF=AE•AF=ab=8,
设C(m,n)(m>0,n>0),则CF=m,OF=n,
将x=m,y=n代入反比例函数y=
得:mn=2,
∴S△OCF=
CF•OF=
mn=1,
同理S△BOE=1,
则S四边形ABOC=S矩形AEOF-S△OCF-S△BOE=8-1-1=6.
故选B
将x=a,y=b代入反比例函数y=
| 8 |
| x |
∴S矩形AEOF=AE•AF=ab=8,
设C(m,n)(m>0,n>0),则CF=m,OF=n,
将x=m,y=n代入反比例函数y=
| 2 |
| x |
∴S△OCF=
| 1 |
| 2 |
| 1 |
| 2 |
同理S△BOE=1,
则S四边形ABOC=S矩形AEOF-S△OCF-S△BOE=8-1-1=6.
故选B
点评:此题考查了反比例函数解析式中k的几何意义,其k的几何意义为:过反比例函数y=
(k≠0)图象上的点作两坐标轴的垂线,两垂线与两坐标轴围成矩形的面积等于|k|,熟练掌握此性质是解本题的关键.
| k |
| x |

练习册系列答案
相关题目
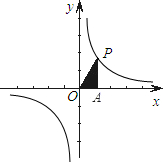 如图,P是双曲线y=
如图,P是双曲线y=| k |
| x |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、-2 |
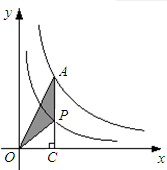 如图,P是双曲线y=
如图,P是双曲线y= (2013•清远模拟)如图点P是双曲线上的一点,过P点分别向x轴,y轴引垂线,得到图中的阴影部分的矩形面积为3,则这个反比例函数的表达式为
(2013•清远模拟)如图点P是双曲线上的一点,过P点分别向x轴,y轴引垂线,得到图中的阴影部分的矩形面积为3,则这个反比例函数的表达式为 如图,P是双曲线y=
如图,P是双曲线y=