题目内容
【题目】如图，在平面直角坐标系中，正方形
的顶点
在
轴正半轴上，顶点
在
轴正半轴上，
、
的长分别是一元二次方程
的两个根（
）．
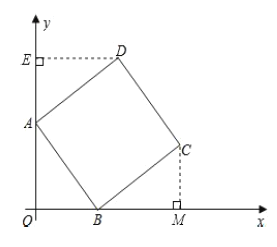
（1）求点
的坐标；
（2）求直线
的解析式；
（3）在直线上是否存在点
，使
为等腰三角形？若存在，请直接写出点的坐标；若不存在，说明理由．
【答案】（1）
（2）
（3）存在，为
，
【解析】
（1）解一元二次方程求出OA、OB的长度，过点D作DE⊥y于点E，根据正方形的性质可得AD=AB，∠DAB=90°，然后求出∠ABO=∠DAE，然后利用“角角边”证明△DAE和△ABO全等，根据全等三角形对应边相等可得DE=OA，AE=OB，再求出OE，然后写出点D的坐标即可；
（2）过点C作CM⊥x轴于点M，同理求出点C的坐标，设直线BC的解析式为y=kx+b（k≠0，k、b为常数），然后利用待定系数法求一次函数解析式解答；
（3）根据正方形的性质，点P与点B重合时，△PCD为等腰三角形；点P为点B关于点C的对称点时，△PCD为等腰三角形，然后求解即可．
解析：（1）
，解得
，
．
，
，
．
过
作
于点
，
正方形
，
，
．
，
，
，
，
，
，，
，
，
，
，
；
（2）过点
作
轴于点
，
同上可证得
，
，
，
，
，
设直线
的解析式为
（
，
、
为常数），
代入
，
得，
，
解得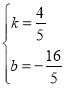
，
；
（3）存在．
点
与点
重合时，，
点与点关于点对称时，．
练习册系列答案
相关题目
