题目内容
如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A、与大圆相
交于点B。小圆的切线AC与大圆相交于点D，且CO平分∠ACB。
（1）试判断BC所在直线与小圆的位置关系，并说明理由；
（2）试判断线段AC、AD、BC之间的数量关系，并说明理由；
（3）若
，求大圆与小圆围成的圆环的面积。（结果保留π）
解：（1）
所在直线与小圆相切，
理由如下：过圆心
作
，垂足为
，
是小圆的切线，
经过圆心，
，又
平分
。
．
所在直线是小圆的切线。
（2）
理由如下：连接
。
切小圆于点
，切小圆于点，
．
在
与
中，
，
（HL） 
。
，
．
（3）
，
．
，
。
圆环的面积
又
， 
。
练习册系列答案
相关题目
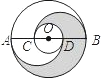如图，在以O为圆心的两个同心圆中，大圆的直径AB交小圆于C、D两点，AC=CD=DB，分别以C、D为圆心，以CD为半径作圆．若AB=6cm，则图中阴影部分的面积为
9、如图，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，已知AB=8，大圆半径为5，则小圆半径为（ ）
（2006•静安区二模）如图，在以O为圆心的两个同心圆中，小圆的半径为1，AB与小圆相切于点A，与大圆相交于B，大圆的弦BC⊥AB，过点C作大圆的切线交AB的延长线于D，OC交小圆于E
如图，在以O为圆心的两个同心圆中，MN为大圆的直径，交小圆于点P、Q，大圆的弦MC交小圆于点A、B．若OM=2，OP=1，MA=AB=BC，则△MBQ的面积为
如图，在以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆的半径为5cm，小圆的半径为3cm，则弦AB的长为（ ）