题目内容
 如图,P是等边△ABC外一点,把BP绕点B顺时针旋转60°到BP′.
如图,P是等边△ABC外一点,把BP绕点B顺时针旋转60°到BP′.(1)请连结AP,求证:△ABP≌△CBP′;
(2)已知∠AP′B=150°,若连结P′P,判断△APP′的形状;
(3)在(2)的条件下,若P′A=2,P′C=3,求PB与P′A的比值是多少.
考点:旋转的性质,等边三角形的判定与性质
专题:
分析:(1)利用旋转的性质得出∠PBA=∠CBP′,进而利用SAS得出全等三角形即可;
(2)利用等边三角形的判定与性质得出∠PP′B=60°,进而求出∠AP′P=90°,即可得出答案;
(3)利用(1)(2)中所求,利用勾股定理得出PP′即可得出答案.
(2)利用等边三角形的判定与性质得出∠PP′B=60°,进而求出∠AP′P=90°,即可得出答案;
(3)利用(1)(2)中所求,利用勾股定理得出PP′即可得出答案.
解答:(1)证明:如图,连接AP,
∵P是等边△ABC外一点,把BP绕点B顺时针旋转60°到BP′,
∴AB=BC,∠PBP′=∠ABC=60°,
∴∠PBA=∠CBP′,
在△ABP和△CBP′中,
,
∴△ABP≌△CBP′(SAS);
(2)解:连接PP′,
∵PB=P′B,∠PBP′=60°,
∴△PBP′是等边三角形,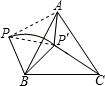
∴∠PP′B=60°,
∵∠AP′B=150°,
∴∠AP′P=90°,
∴△APP′是直角三角形;
(3)解:∵△PBP′是等边三角形,
∴PP′=PB=P′B,
∵△ABP≌△CBP′,
∴AP=P′C=3,
在Rt△AP′P中
PP′=
=
=
,
∴PB=
,
∴PB与P′A的比值是:
:2.
∵P是等边△ABC外一点,把BP绕点B顺时针旋转60°到BP′,
∴AB=BC,∠PBP′=∠ABC=60°,
∴∠PBA=∠CBP′,
在△ABP和△CBP′中,
|
∴△ABP≌△CBP′(SAS);
(2)解:连接PP′,
∵PB=P′B,∠PBP′=60°,
∴△PBP′是等边三角形,

∴∠PP′B=60°,
∵∠AP′B=150°,
∴∠AP′P=90°,
∴△APP′是直角三角形;
(3)解:∵△PBP′是等边三角形,
∴PP′=PB=P′B,
∵△ABP≌△CBP′,
∴AP=P′C=3,
在Rt△AP′P中
PP′=
| AP2-P′A2 |
| 32-22 |
| 5 |
∴PB=
| 5 |
∴PB与P′A的比值是:
| 5 |
点评:此题主要考查了旋转的性质以及勾股定理和全等三角形的判定与性质等知识,熟练利用旋转的性质得出对应角以及对应边关系是解题关键.

练习册系列答案
相关题目
不一定在三角形内部的线段是( )
| A、三角形的角平分线 |
| B、三角形的中线 |
| C、三角形的高 |
| D、以上皆不对 |
 如图,已知梯形ABCD中,AD∥BC,tanB=1,tanC=2,AD=6,BC=10,求梯形的高.
如图,已知梯形ABCD中,AD∥BC,tanB=1,tanC=2,AD=6,BC=10,求梯形的高. 如图,正方形ABCD边长为4,点E在边AB上(点E与点A、B不重合),过点A作AF⊥DE,垂足为G,AF与边BC相交于点F.
如图,正方形ABCD边长为4,点E在边AB上(点E与点A、B不重合),过点A作AF⊥DE,垂足为G,AF与边BC相交于点F.