题目内容
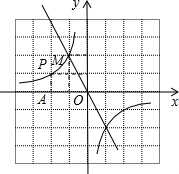 如图,M点是正比例函数y=kx和反比例函数y=
如图,M点是正比例函数y=kx和反比例函数y=| m |
| x |
(1)求这两个函数的解析式;
(2)在反比例函数y=
| m |
| x |
分析:(1)从图象上可看到正比例函数y=kx和反比例函数y=
都过(1,2)点,从而可求出函数式.
(2)P是反比例函数上的一点,过点P做PA垂直于x轴,垂足为A,所以△OPA的面积是
m,点Q是直线MO上一点,QB垂直于y轴,垂足为B,Q点的坐标为(x,kx),所以根据△OBQ的面积是△OPA的面积的2倍可列方程求解.
| m |
| x |
(2)P是反比例函数上的一点,过点P做PA垂直于x轴,垂足为A,所以△OPA的面积是
| 1 |
| 2 |
解答:解:(1)∵y=kx过(-1,2)点,
∴k=-2,
∴y=-2x.
∵y=
过(-1,2)点,
∴m=-2.
∴y=-
;
(2)∵△OPA的面积是
m=1,Q点的坐标为(x,-2x),
∴
•|x|•|-2x|=2,
x=±
,
因为在第二象限所以Q点的坐标为(-
,2
),或(
,-2
).
∴k=-2,
∴y=-2x.
∵y=
| m |
| x |
∴m=-2.
∴y=-
| 2 |
| x |
(2)∵△OPA的面积是
| 1 |
| 2 |
∴
| 1 |
| 2 |
x=±
| 2 |
因为在第二象限所以Q点的坐标为(-
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查反比例函数的综合运用,关键能够熟练确定函数式,并能够掌握由函数图象上的点作为顶点的三角形面积和函数坐标之间的关系.

练习册系列答案
相关题目
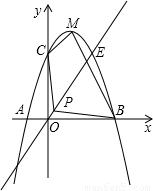
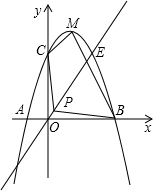 顶点为M,又正比例函数y=kx的图象于二次函数相交于两点D、E,且P是线段DE的中点.
顶点为M,又正比例函数y=kx的图象于二次函数相交于两点D、E,且P是线段DE的中点.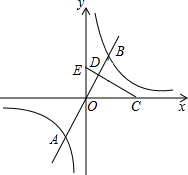 如图,已知正比例函数y=ax(a≠0)的图象与反比例函致
如图,已知正比例函数y=ax(a≠0)的图象与反比例函致 为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.
为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点. 】
】
 (k≠0)的图象的一个交点为A(-1,2-k2),另—个交点为B,且A、B关于原点O对称,D为OB的中点,过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E.
(k≠0)的图象的一个交点为A(-1,2-k2),另—个交点为B,且A、B关于原点O对称,D为OB的中点,过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E.