题目内容
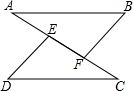如图，点E、F在AC上，AB∥CD，AB=CD，AE=CF，求证：∠B=∠D．
证明：∵AB∥CD，
∴∠A=∠C，
∵AE=CF，
∴AE+EF=CF+EF，
∴AF=CE，
在△ABF和△CDE中
∴△ABF≌△CDE（SAS），
∴∠B=∠D．
分析：根据平行线性质得出∠A=∠C，求出AF=CE，根据SAS证出△ABF≌△CDE即可．
点评：本题考查了平行线性质，全等三角形的性质和判定的应用，注意：全等三角形的性质是：①全等三角形的对应边相等，对应角相等，②全等三角形的判定定理有SAS，ASA，AAS，SSS．
∴∠A=∠C，
∵AE=CF，
∴AE+EF=CF+EF，
∴AF=CE，
在△ABF和△CDE中
∴△ABF≌△CDE（SAS），
∴∠B=∠D．
分析：根据平行线性质得出∠A=∠C，求出AF=CE，根据SAS证出△ABF≌△CDE即可．
点评：本题考查了平行线性质，全等三角形的性质和判定的应用，注意：全等三角形的性质是：①全等三角形的对应边相等，对应角相等，②全等三角形的判定定理有SAS，ASA，AAS，SSS．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，点D、E分别在AC、BC上，如果测得CD=20m，CE=40m，AD=100m，BE=20m，DE=45m，
11、如图，点D、E分别在AC、AB上，已知AB=AC，添加下列条件，不能说明△ABD≌△ACE的是（ ）
如图，点D、E在AC、AB上，且AD=AE，∠B=∠C，那么BE=CD吗？为什么？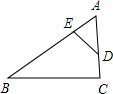
如图，点D、E分别在AC、AB上，已知AE=3，AD=4，AB=8，则AC=
如图，点D、E分别在AC、AB上，给出下列四组条件：