题目内容
如图，△ABC为⊙O的内接三角形，∠ACB=50°，则∠ABO的度数等于
- A.40°
- B.50°
- C.60°
- D.25°
A
分析：先根据圆周角定理求出∠AOB的度数，再由三角形内角和定理求出∠ABO的度数即可．
解答：∵∠ACB=50°，
∴∠AOB=2∠ACB=2×50°=100°，
∵OA=OB，
∴∠ABO=
=
=40°．
故选A．
点评：本题考查的是圆周角定理，在解答此题时往往用到三角形的内角和是180°这一隐含条件．
分析：先根据圆周角定理求出∠AOB的度数，再由三角形内角和定理求出∠ABO的度数即可．
解答：∵∠ACB=50°，
∴∠AOB=2∠ACB=2×50°=100°，
∵OA=OB，
∴∠ABO=
==40°．故选A．
点评：本题考查的是圆周角定理，在解答此题时往往用到三角形的内角和是180°这一隐含条件．
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
种不同的平行四边形，并计算其中一种平行四边形的对角线的长．
5、如图，△ABC为⊙O的内接三角形，AB是直径，∠A=20°，则∠B的度数是（ ）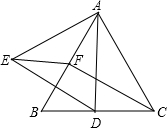
如图，△ABC为等边三角形，D、F分别为BC、AB上的点，且CD=BF，以AD为边作等边△ADE．
22、如图，△ABC为等边三角形，又DE⊥BC，EF⊥AC，FD⊥AB，垂足分别为E，F，D，则△DEF是等边三角形吗？说明你的理由．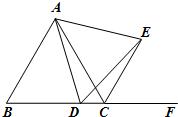
23、如图，△ABC为等边三角形，D为BC上一点，∠ADE=60°，DE交∠ACB外角平分线于E．