题目内容
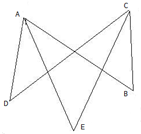 线段AB、CD相交于点O,AE平分∠BCD,CE平分∠BCD,当∠B=α,角∠D=β时,∠E的度数为
线段AB、CD相交于点O,AE平分∠BCD,CE平分∠BCD,当∠B=α,角∠D=β时,∠E的度数为考点:角平分线的性质
专题:
分析:根据角平分线的定义得到∠1=∠2,∠3=∠4,再根据(1)中的结论得到∠1+∠D=∠3+∠E,∠2+∠E=∠4+∠B,两等式相减得到∠D-∠E=∠E-∠B,由此可得出结论.
解答:解:∵∠DAB和∠BCD的平分线AE和CE相交于点E,
∴∠1=∠2,∠3=∠4,
∵∠1+∠D=∠3+∠E,∠2+∠E=∠4+∠B,
∴∠D-∠E=∠E-∠B,即∠E=
(∠D+∠B)=
α+
β,
故答案为:
α+
β.

∴∠1=∠2,∠3=∠4,
∵∠1+∠D=∠3+∠E,∠2+∠E=∠4+∠B,
∴∠D-∠E=∠E-∠B,即∠E=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
 如图,AM、AN分别切⊙O于M、N两点,点B在⊙O上,且∠MBN=60°,则∠A的度数是( )
如图,AM、AN分别切⊙O于M、N两点,点B在⊙O上,且∠MBN=60°,则∠A的度数是( )| A、60° | B、70° |
| C、80° | D、140° |
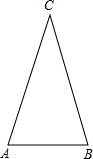 如图,在△ABC中,AC=BC=1,∠C=36°,求面积S△ABC.
如图,在△ABC中,AC=BC=1,∠C=36°,求面积S△ABC.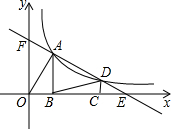 如图,点A,D是函数y=
如图,点A,D是函数y= 如图,在平面直角坐标系中,点O是坐标原点,四边形ABCD是菱形,点B、点C在x轴上,点A在y轴上,BD交y轴于点M,点A的坐标为(0,4),点B的坐标为(-3,0).
如图,在平面直角坐标系中,点O是坐标原点,四边形ABCD是菱形,点B、点C在x轴上,点A在y轴上,BD交y轴于点M,点A的坐标为(0,4),点B的坐标为(-3,0).