题目内容
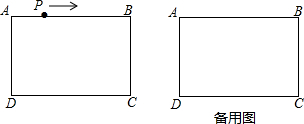
7．
如图，矩形ABCD中，AD=5，AB=8，点E为射线DC上一个动点，把△ADE沿AE折叠，点D的对应点为D′，当点D′刚好落在线段BC的垂直平分线上时，求线段DE的长．
分析 根据已知条件得到D′D=AD′=AD，运用勾股定理即可解决问题．
解答 
解：如图，连接D′D，
∵点D′在BC的垂直平分线上，
∴点D′在AD的垂直平分线上，
∴D′D=AD′=AD；
设DE为x，易得AE=2x，
由勾股定理得：（2x）2-x2=52，
∴x=$\frac{5\sqrt{3}}{3}$．
∴DE=$\frac{5}{3}$$\sqrt{3}$．
点评 本题考查了矩形的性质、翻折变换的性质、勾股定理，对综合的分析问题解决问题的能力提出了较高的要求．
练习册系列答案
相关题目
抛物线y=-x2+bx+c的部分图象如图所示．
10．一根绳子剪去$\frac{1}{4}$，恰好是$\frac{1}{5}$米，这根绳子长多少米？正确的列式是（ ）
| A． | $\frac{1}{4}$×$\frac{1}{5}$ | B． | $\frac{1}{4}$+$\frac{1}{5}$ | C． | $\frac{1}{4}$÷$\frac{1}{5}$ | D． | $\frac{1}{5}$÷$\frac{1}{4}$ |
抛物线y=ax2+bx+c交x轴于A，B两点，交y轴于点C顶点为D，已知：D（-1，-4），A（-3，0）．
如图，已知点P是射线ON上一动点（即P可在射线ON上运动），∠AON=30°，当∠A=60°或90°时，△AOP为直角三角形．