题目内容
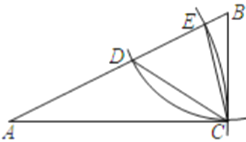
【题目】如图,在![]() 中,
中,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交线段
长为半径画弧,交线段![]() 于点
于点![]() ,连接
,连接![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交线段
长为半径画弧,交线段![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求![]() 的度数.
的度数.
(2)设![]() .
.
①线段![]() 的长是关于
的长是关于![]() 的方程
的方程![]() 的一个根吗?说明理由.
的一个根吗?说明理由.
②若![]() 为
为![]() 的中点,求
的中点,求![]() 的值.
的值.
【答案】(1)45°;(2)①是,理由见解析;②![]() .
.
【解析】
(1)根据等腰三角形的性质可得![]() ,
,![]() ,根据∠ACB=90°及三角形内角和定理即可得答案;
,根据∠ACB=90°及三角形内角和定理即可得答案;
(2)①利用勾股定理可用a、b表示出AB的长,进而可表示出BE的长,利用公式法可得出方程![]() 的两个根,即可得答案;
的两个根,即可得答案;
②由D为AE中点可得AD=![]() ,即可得出AB=
,即可得出AB=![]() +a,利用勾股定理即可得答案.
+a,利用勾股定理即可得答案.
(1)由作图可知:BC=BD,AC=AE,
∴![]() ,
,![]() ,
,
∵![]()
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() .
.
(2)①线段![]() 的长是关于
的长是关于![]() 的方程
的方程![]() 的一个根.
的一个根.
理由如下:
由勾股定理得:![]() ,
,
∵AE=AC=b,
∴![]() ,
,
解关于![]() 的方程
的方程![]() 得:
得:![]()
∴线段![]() 的长是关于
的长是关于![]() 的方程
的方程![]() 的一个根.
的一个根.
②∵点D为![]() 的中点,
的中点,
∴![]() ,
,
∴AB=![]() ,
,
∴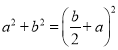 ,
,
整理得:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某中学九(2)班同学为了了解2019年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
月均用水量 | 频数 | 频率 |
| 6 | 0.12 |
| ________ | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | ________ |
| 2 | 0.04 |

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)月均用水量的中位数落在第________小组;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20吨的家庭大约有多少户?





