题目内容
 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=2,AB=3,那么cos∠BCD的值为
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=2,AB=3,那么cos∠BCD的值为考点:锐角三角函数的定义
专题:
分析:首先利用勾股定理计算出BC长,然后再利用直角三角形的面积公式计算出CD长,再用余弦定义可得答案.
解答:解:∵AC=2,AB=3,∠ACB=90°,
∴BC=
=
,
∵
AB•CD=
AC•BC,
∴3CD=2
,
CD=
,
∴cos∠BCD=
=
=
,
故答案为:
.
∴BC=
| 32-22 |
| 5 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴3CD=2
| 5 |
CD=
2
| ||
| 3 |
∴cos∠BCD=
| DC |
| BC |
| ||||
|
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:此题主要考查了锐角三角函数的定义,以及勾股定理的应用,关键是掌握余弦=
.
| 邻边 |
| 斜边 |

练习册系列答案
相关题目
在平行四边形、矩形、等边三角形、正方形四种图形中,既是轴对称图形又是中心对称图形的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,已知二次函数y=ax2+bx+c的图象的顶点为M(2,1),且过点N(3,2).
如图,已知二次函数y=ax2+bx+c的图象的顶点为M(2,1),且过点N(3,2). 在平面直角坐标系xOy(如图)中,已知:点A(3,0)、B(-2,5)、C(0,-3).
在平面直角坐标系xOy(如图)中,已知:点A(3,0)、B(-2,5)、C(0,-3).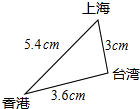 在中国地图册上,联结上海、香港、台湾三地构成一个三角形,用刻度尺测得它们之间的距离如图所示.飞机从台湾直飞上海的距离约为l290千米,那么飞机从台湾绕道香港再到上海的空中飞行距离是
在中国地图册上,联结上海、香港、台湾三地构成一个三角形,用刻度尺测得它们之间的距离如图所示.飞机从台湾直飞上海的距离约为l290千米,那么飞机从台湾绕道香港再到上海的空中飞行距离是 河堤横截面如图所示,堤高BC为4米,迎水坡AB的坡比为1:
河堤横截面如图所示,堤高BC为4米,迎水坡AB的坡比为1: 在一个边长为4cm正方形里作一个扇形(如图所示),再将这个扇形剪下卷成一个圆锥的侧面,则这个圆锥的高为
在一个边长为4cm正方形里作一个扇形(如图所示),再将这个扇形剪下卷成一个圆锥的侧面,则这个圆锥的高为