题目内容
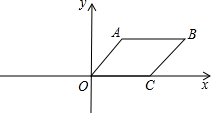
 平行四边形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,
平行四边形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°, ,则点B的坐标是
,则点B的坐标是
- A.(3,1)
- B.(1,3)
- C.(2,1)
- D.(1,2)
A
分析:过C作CE⊥OA,过B作BF⊥OA,先利用三角函数求出OE、CE的长度,从而得出C点纵坐标坐标,然后利用平行四边形的性质求得点B的坐标.
解答:过C作CE⊥OA,过B作BF⊥OA,
由题意可得OC= ,∠AOC=45°,
,∠AOC=45°,
∴OD=1,CE=1,
∵四边形OABC是平行四边形,
∴BC∥OA,
∴B和C的纵坐标相等,
∴B的纵坐标为1,
∵AF=1,
∵OA=2,
∴OF=3,
∴点B的横坐标坐标是3,
∴点B的坐标是(3,1),
故选A.
点评:本题综合考查了平行四边形的性质和坐标的确定,解答本题的关键有两点,①掌握平行四边形的性质②理解三角函数的定义,及各三角函数在直角三角形中的表示形式.
分析:过C作CE⊥OA,过B作BF⊥OA,先利用三角函数求出OE、CE的长度,从而得出C点纵坐标坐标,然后利用平行四边形的性质求得点B的坐标.
解答:过C作CE⊥OA,过B作BF⊥OA,
由题意可得OC=
 ,∠AOC=45°,
,∠AOC=45°,∴OD=1,CE=1,
∵四边形OABC是平行四边形,

∴BC∥OA,
∴B和C的纵坐标相等,
∴B的纵坐标为1,
∵AF=1,
∵OA=2,
∴OF=3,
∴点B的横坐标坐标是3,
∴点B的坐标是(3,1),
故选A.
点评:本题综合考查了平行四边形的性质和坐标的确定,解答本题的关键有两点,①掌握平行四边形的性质②理解三角函数的定义,及各三角函数在直角三角形中的表示形式.

练习册系列答案
相关题目
 如图,在平行四边形OABC中,已知
如图,在平行四边形OABC中,已知 平行四边形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,
平行四边形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°, 如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,顶点B的坐标为(6,4).若直线l经过点(1,0),且将平行四边形OABC分割成面积相等的两部分,则直线l的函数解析式是
如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,顶点B的坐标为(6,4).若直线l经过点(1,0),且将平行四边形OABC分割成面积相等的两部分,则直线l的函数解析式是