Question

如图，已知EF⊥BC，∠1=∠C，∠2+∠3=180°．试说明直线AD与BC垂直．（请在下面的解答过程的空格内填空或在括号内填写理由）．
理由：
∵∠1=∠C，（ 已知 ）
∴________∥________，________
∴∠2=________．________
又∵∠2+∠3=180°，（ 已知 ）
∴∠3+________=180°．（ 等量代换 ）
∴________∥________，________
∴∠ADC=∠EFC．________
∵EF⊥BC，（ 已知 ）
∴∠EFC=90°，
∴∠ADC=90°，
∴________⊥________．

Answer 1

GD    AC    同位角相等，两直线平行    ∠DAC    两直线平行，内错角相等    ∠DAC    AD    EF    同旁内角互补，两直线平行    两直线平行，同位角相等    AD    BC
分析：结合图形，根据平行线的判定和性质逐一进行填空即可．
解答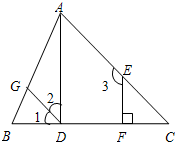：解：∵∠1=∠C，（已知）
∴GD∥AC，（同位角相等，两直线平行）
∴∠2=∠DAC．（两直线平行，内错角相等）
又∵∠2+∠3=180°，（已知）
∴∠3+∠DAC=180°．（等量代换）
∴AD∥EF，（同旁内角互补，两直线平行）
∴∠ADC=∠EFC．（两直线平行，同位角相等）
∵EF⊥BC，（已知 ）
∴∠EFC=90°，
∴∠ADC=90°，
∴AD⊥BC．
点评：本题主要考查了平行线的判定和性质，已经垂线的定义，解答此题的关键是注意平行线的性质和判定定理的综合运用．