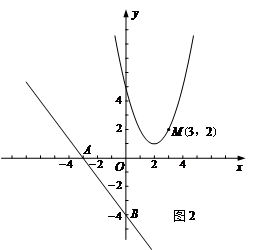题目内容
已知二次函数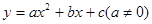 的图象如图所示,
的图象如图所示,
下列结论:①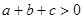 ②
② ③
③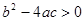 ④
④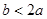 ⑤
⑤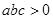
其中正确的有( )个
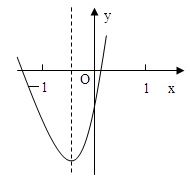
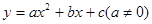 的图象如图所示,
的图象如图所示,下列结论:①
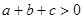 ②
② ③
③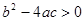 ④
④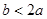 ⑤
⑤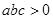
其中正确的有( )个

| A.1 | B.2 | C.3 | D.4 |
C
试题分析:由题意可知,
 ,对称轴是
,对称轴是 。所以
。所以 ,当x=0时,c在x轴下方,所以
,当x=0时,c在x轴下方,所以 ,由于函数和x轴有两个焦点,所以
,由于函数和x轴有两个焦点,所以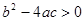 ,所以
,所以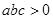 错误,故符合条件的有3个,故选C
错误,故符合条件的有3个,故选C点评:本题属于对数形结合思想的综合考查和运用分析

练习册系列答案
相关题目
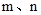 是方程
是方程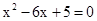 的两个实数根,且
的两个实数根,且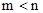 ,抛物线
,抛物线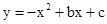 的图像经过点A(
的图像经过点A(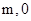 )、B(
)、B(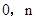 ).
).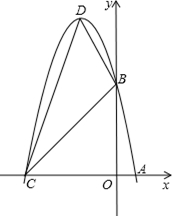
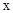 轴的另一交点为C,抛物线的顶点为D,
轴的另一交点为C,抛物线的顶点为D,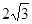 ),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.
),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.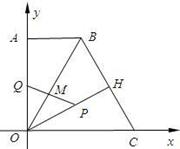
 ,将∠ABC对折,使点C的对应点H恰好落在直线AB上,折痕交AC于点O,以点O为坐标原点,AC所在直线为x轴建立平面直角坐标系
,将∠ABC对折,使点C的对应点H恰好落在直线AB上,折痕交AC于点O,以点O为坐标原点,AC所在直线为x轴建立平面直角坐标系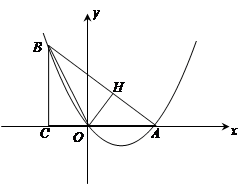
 ,
, 图象的是
图象的是
 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.
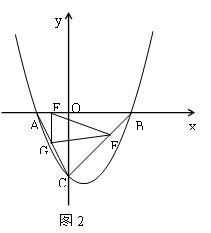
 个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的
个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的 ?
? 交x轴于点Q、M,交y轴于点P,点P关于x轴的对称点为N。
交x轴于点Q、M,交y轴于点P,点P关于x轴的对称点为N。
 交
交 轴于点
轴于点 ,交
,交 轴于点
轴于点 ,在
,在 ,它们关于
,它们关于 在
在 于点
于点 ,
, 于点
于点 ,四边形
,四边形 与四边形
与四边形 的面积分别为6和10,则
的面积分别为6和10,则 与
与 的面积之和为 .
的面积之和为 .
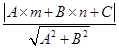 .
.
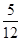 x-
x- 的距离d时,先将y=
的距离d时,先将y= =
= .
.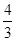 x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).