题目内容
如图，海滨浴场A点处发现B点有人求救，1号救生员从A点前往营救；2号沿直线岸边向前跑到C点再前往营救；3号救生员沿直线岸边向前跑300米到离B点最近的D点再前往营救．救生员在岸边跑的速度都是6米/秒，他们水中游泳速度都是2米/秒．若∠BAD=45°，∠BCD=60°，三名救生员同时从A点出发，请说明谁先到达B点？
分析：因为速度已知，比较时间，需求路程，即求AB、AC、BC、BD的长以后再计算时间进行比较，解直角三角形ABD和BCD．
解答：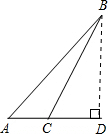
解：如图，在△ABD中，∠A=45°，∠D=90°，AD=300，
∴AB=AD÷cos45°=300
，
BD=AD•tan45°=300．
在△BCD中，∵∠BCD=60°，∠D=90°，
∴BC=BD÷sin60°=300÷
=200
，
∴CD=BD÷tan60°=300÷
=100
．
1号救生员到达B点所用的时间为 300
÷2=150
≈210（秒）；
2号救生员到达B点所用的时间为 （300-100
）÷6+200
÷2=50+250
÷3≈191.7（秒）；
3号救生员到达B点所用的时间为 300÷6+300÷2=200（秒）．
∵191.7＜200＜210，
∴2号救生员先到达营救地点B．
解：如图，在△ABD中，∠A=45°，∠D=90°，AD=300，∴AB=AD÷cos45°=300
| 2 |
BD=AD•tan45°=300．
在△BCD中，∵∠BCD=60°，∠D=90°，
∴BC=BD÷sin60°=300÷
| ||
| 2 |
| 3 |
∴CD=BD÷tan60°=300÷
| 3 |
| 3 |
1号救生员到达B点所用的时间为 300
| 2 |
| 2 |
2号救生员到达B点所用的时间为 （300-100
| 3 |
| 3 |
| 3 |
3号救生员到达B点所用的时间为 300÷6+300÷2=200（秒）．
∵191.7＜200＜210，
∴2号救生员先到达营救地点B．
点评：本题考查了方向角的应用，所求问题较多，应认真审题，理顺关系．
练习册系列答案
阅读快车系列答案
相关题目
如图，某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救，便立即派三名救生员前去营救，1号救生员从A点直接跳入海中；2号救生员沿岸边（岸边看成是直线）向前跑到C点，再跳入海中；3号救生员沿岸边向前跑300米到离B点最近的D点，再跳入海中，救生员在岸上跑的速度都是6米/秒，在水中游泳的速度都是2米/秒，若∠BAD=45°，∠BCD=60°，三名救生员同时从A点出发，请说明谁先到达营救地点B．（参考数据：
如图，某海滨浴场岸边A点处发现海中B点有人求救，便立即派出两名救生员前去营救，1号救生员从A点直接跳入海中，2号救生员沿岸边向前跑100米到离B点最近的C点，再跳入海中．救生员在岸上跑的速度为5米/秒，水中游泳的速度为2米/秒，若∠BAC=60°，两名救生员同时从A点出发，请说明谁先到达营救地点B．（参考数据
如图，海滨浴场A点处发现B点有人求救，1号救生员从A点前往营救；2号沿直线岸边向前跑到C点再前往营救；3号救生员沿直线岸边向前跑300米到离B点最近的D点再前往营救．救生员在岸边跑的速度都是6米/秒，他们水中游泳速度都是2米/秒．若∠BAD=45°，∠BCD=60°，三名救生员同时从A点出发，请说明谁先到达B点？