��Ŀ����
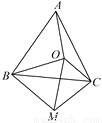
��ͼ����OΪ�ȱ�������ABC��һ�㣬����OA��OB��OC����OBΪһ������OBM��60�㣬��BO��BM������CM��OM.
(1)�ж�AO��CM�Ĵ�С��ϵ��֤����
(2)��OA��8��OC��6��OB��10���жϡ�OMC����״��֤����
��ϰ��ϵ�д�
 �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д� ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д�
�����Ŀ
��Ŀ����
��ͼ����OΪ�ȱ�������ABC��һ�㣬����OA��OB��OC����OBΪһ������OBM��60�㣬��BO��BM������CM��OM.
(1)�ж�AO��CM�Ĵ�С��ϵ��֤����
(2)��OA��8��OC��6��OB��10���жϡ�OMC����״��֤����

 �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д� ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д�