题目内容
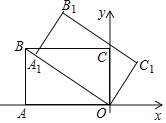
【题目】如图，平面直角坐标系中，矩形
的对角线
，
．
(1)把矩形沿直线
对折，使点
落在点
处，折痕分别与
、
、
相交于点
、
、
，求直线的解析式；
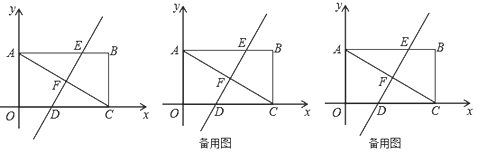
(2)若点
在直线上，平面内是否存在点
，使以
、、、为顶点的四边形是菱形？若存在，请直接写出点的坐标；若不存在，请说明理由．
【答案】（1）
；（2）存在；N点坐标为：
，
，
.
【解析】
（1）由含30度直角三角形性质，得OA=
AC=12，然后求出OC，然后求得直线AC的解析式，由折叠知DE⊥AC，点F是AC中点，然后可以求得DE的解析式；
（2）分为①以OF，FM为边；②以FM为边，OF为对角线；③以OF为边，FM为对角线，三类进行讨论分析，然后可求N点坐标．
解：（1）根据题意，在直角三角形AOC中，∠AOC=90°，
，
，
∴
，即点A为：（0，12），
由勾股定理，得
，即点C为：（
），
设直线AC的方程为
，把A、C坐标代入，得
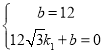，解得：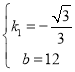
，
∴直线AC的方程为：
，
根据折叠的性质，有DE⊥AC，点F是AC中点，
∴直线DE的斜率为：
，点F为（
），
则设直线DE的解析式为
，把点F代入，得
，解得：
，
∴直线DE的解析式为：；
（2）存在；
①以OF，FM为边，如图
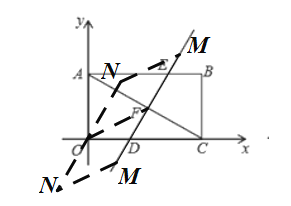
由（1）知，直线DE的解析式为：，
令
，则
，
∴点D坐标为：
，
∵ONMF是菱形
∴OF=ON，ON∥DE
∴直线ON的解析式为：
，
设N点坐标为：（
），
∴
，
，
∴
，
解得：
，
∴N点坐标为：
；
②以FM为边，OF为对角线；连接AD，CE，如图：
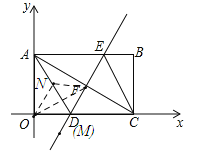
由折叠知，四边形ADCE是菱形，
∴AD=CD=
，
∴∠DAC=∠DCA=30°，
∴∠OAD=30°，
∴∠OAD=∠DAC，AD=AD，∠AOD=∠AFD=90°，
∴△AOD≌△AFD，
∴AO=AF，OD=FD，
∴AD是OF 的垂直平分线，
∵四边形ONFM是菱形，
∴MN是OF的垂直平分线，
∴M与D重合，即M为，
设N为
，
∵OF与MN互相平分，
∴
，
，
解得：
，
∴N点坐标为：；
③以OF为边，FM为对角线，如图：
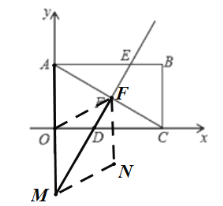
∵直线DE的解析式为：，
∴直线DE与y轴的交点为（0，-12），
∵四边形OFNM是菱形，
，
∴OM=OF=12，
∴点M的坐标为（0，-12），
∵OM∥FN，OM=FN=12，且点F为（），
∴N点坐标为：；
综合上述，N点坐标为：，，.
新课标阶梯阅读训练系列答案
