题目内容
 如图,在平面直角坐标系xOy中,?OABC的顶点A,B的坐标分别为(6,0),(7,3),将?OABC绕点O逆时针方向旋转得到?OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为
如图,在平面直角坐标系xOy中,?OABC的顶点A,B的坐标分别为(6,0),(7,3),将?OABC绕点O逆时针方向旋转得到?OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为考点:平行四边形的性质,坐标与图形变化-旋转
专题:
分析:如图,过点C作CD⊥OC′于点D.利用旋转的性质和面积法求得OD=
,然后通过解直角三角形推知:tan∠COC′=
.结合图形和旋转的性质得到∠COC′=∠AOE,自点E向x轴引垂线,交x轴于点F.则EF=3.利用等角的正切值相等tan∠AOE=tan∠COC′=
=
.易求OF的长度,则C′E=O′E+O′C=4+1=5.
| 6 | ||
|
| 3 |
| 4 |
| EF |
| OF |
| 3 |
| 4 |
解答: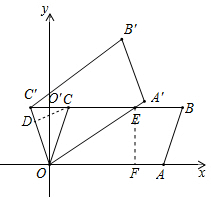 解:∵OC=OC′,CC′⊥y轴,A,B的坐标分别为(6,0),(7,3),
解:∵OC=OC′,CC′⊥y轴,A,B的坐标分别为(6,0),(7,3),
∴点C到y轴的距离:7-6=1.
∴O′C=O′C′=1,O点到CC′的距离是3,
∴OD=DC′=
,S△OCC′=
×2×3=3.
如图,过点C作CD⊥OC′于点D.则
OD•C′D=3,
∴OD=
,sin∠COC′=
=
,tan∠COC′=
.
∵∠COC′+∠COE=∠AOE+∠COE,
∴∠COC′=∠AOE,
∴tan∠AOE=tan∠COC′=
.
自点E向x轴引垂线,交x轴于点F.则EF=3.
∵tan∠AOE=
,
∴OF=
=4,
∵OF=O′E=4,
∴C′E=O′E+O′C′=4+1=5.
故答案是:5.
 解:∵OC=OC′,CC′⊥y轴,A,B的坐标分别为(6,0),(7,3),
解:∵OC=OC′,CC′⊥y轴,A,B的坐标分别为(6,0),(7,3),∴点C到y轴的距离:7-6=1.
∴O′C=O′C′=1,O点到CC′的距离是3,
∴OD=DC′=
| 10 |
| 1 |
| 2 |
如图,过点C作CD⊥OC′于点D.则
| 1 |
| 2 |
∴OD=
| 6 | ||
|
| OD |
| OC |
| 3 |
| 5 |
| 3 |
| 4 |
∵∠COC′+∠COE=∠AOE+∠COE,
∴∠COC′=∠AOE,
∴tan∠AOE=tan∠COC′=
| 3 |
| 4 |
自点E向x轴引垂线,交x轴于点F.则EF=3.
∵tan∠AOE=
| EF |
| OF |
∴OF=
| EF |
| tan∠AOE |
∵OF=O′E=4,
∴C′E=O′E+O′C′=4+1=5.
故答案是:5.
点评:本题考查了平行四边形的性质和旋转的性质.根据题意作出辅助线是解题的关键与难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个口袋中有2个红球,3个白球,这些球除色外都相同,从口袋中随机摸出一个球,这个球是红球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法正确的是( )
| A、有理数都是有限小数 |
| B、所有的无理数都是无限小数 |
| C、带根号的数都是无理数 |
| D、无限小数都是无理数 |
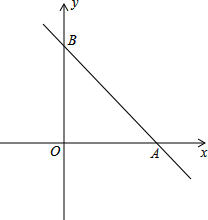 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=- 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点). 某校准备在校内倡导“光盘行动”,随机调查了部分同学某年餐后饭菜的剩余情况,调查数据的部分统计结果如表:
某校准备在校内倡导“光盘行动”,随机调查了部分同学某年餐后饭菜的剩余情况,调查数据的部分统计结果如表: