��Ŀ����
����Ŀ����������һ����������һ��������Ա��ཻ�������뽻��֮����߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ߣ�
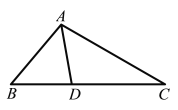
��1����ͼ���ڡ�ABC�У�ADΪ��ƽ���ߣ���B=50�㣬��C=30������֤��ADΪ��ABC�������ߣ�
��2���ڡ�ABC�У���B=46�㣬AD�ǡ�ABC�������ߣ��ҡ�ABD����ABΪ���ĵ��������Σ����BAC�Ķ�����
���𰸡���1������������2����BAC�Ķ���Ϊ113�㣮
��������
������һ���¶���ͼ�ε��⡣
��1�����������ε������ߵĶ��壬ֻҪ֤����ABD�ǵ��������Σ���CAD�ס�CBA���ɽ�����⣮
��2����ͼ2�У���������������������AB=AD����CAD�ס�CBA�����B=��ADB=��CAD����AC��BC��������ABC�������ì�ܣ�����AB=BD����CAD�ס�CBA.
��1��֤������![]() ��
��![]() ��
��
��![]() .
.
��ADΪ��ƽ������
��![]() .
.
��![]() .
.
��![]() .
.
����ABD�ǵ���������.
��![]() ��
��![]() ��
��
���CAD�ס�CBA.
��ADΪ��ABC�������ߣ�
��2����AD�ǡ�ABC�������ߣ��ҡ�ABD����ABΪ���ĵ��������Σ�
���CAD�ס�CBA.
��![]() .
.
�ߡ�ABD����ABΪ���ĵ��������Σ�
���������:
��AB=ADʱ��
��![]() .
.
�֡�![]() ��
��
��![]() �����������⣬�������������.
�����������⣬�������������.
��AB=BDʱ��
��![]() .
.
��![]() .
.
����BAC�Ķ���Ϊ![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�