题目内容
矩形ABCD的两条对角线相交于点O，如果矩形的周长是34cm，又△AOB的周长比△ABC的周长少7cm，则AB=________cm，BC=________cm．
10 7
分析：根据矩形的对边相等以及所给的三角形的周长可得到和所求线段相关的两个式子，进而求解．
解答：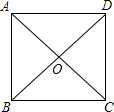
解：设AB=a，BC=b．
∴2OA=2OB=AC=
，2a+2b=34，即a+b=17．
由题意可知△AOB的周长+7=△ABC的周长．
∴AB+OA+OB+7=AB+BC+AC．
∴a++7=a+b+．
即b=7，a=17-7=10．即AB=10，BC=7．
故答案为，10，7．
点评：本题综合考查了矩形的性质及勾股定理的运用．
分析：根据矩形的对边相等以及所给的三角形的周长可得到和所求线段相关的两个式子，进而求解．
解答：
解：设AB=a，BC=b．∴2OA=2OB=AC=
，2a+2b=34，即a+b=17．由题意可知△AOB的周长+7=△ABC的周长．
∴AB+OA+OB+7=AB+BC+AC．
∴a+
+7=a+b+．即b=7，a=17-7=10．即AB=10，BC=7．
故答案为，10，7．
点评：本题综合考查了矩形的性质及勾股定理的运用．
练习册系列答案
相关题目
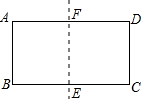如图所示，将矩形ABCD沿两条较长边的中点的连线对折，如果矩形BEFA与矩形ABCD相似，那么AB：AD等于（ ）A、
| ||
B、1：
| ||
C、
| ||
D、1：
|
请将下面证明中每一步的理由填在括号内：
