��Ŀ����
��ͼ
 ������
������
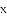
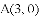
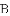
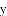
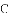
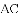
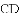
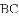
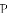
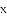


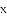
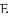
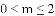
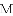
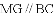
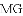
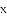
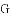
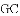
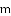
 �У�
��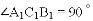 ��
��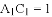 ��
��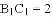 ��ֱ�DZ�
��ֱ�DZ�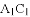 ��
��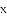
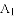 ��
��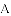
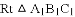 ��
��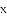
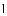
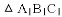 ��
��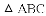
 ʱ��
ʱ�� �ƶ���ʱ��
�ƶ���ʱ��
��ϰ��ϵ�д�
�����Ŀ
һ�����������۳ɱ�Ϊ20Ԫ/ǧ�˵�ij��Ʒ��������۲��Ź涨���ò�Ʒÿǧ���ۼ۲��ó���90Ԫ�������۹����з��ֵ�����y��ǧ�ˣ����ۼ�x��Ԫ/ǧ�ˣ�����һ�κ�����ϵ����Ӧ��ϵ���±���
�ۼ�x��Ԫ/ǧ�ˣ� | �� | 50 | 60 | 70 | 80 | �� |
������y��ǧ�ˣ� | �� | 100 | 90 | 80 | 70 | �� |
��1����y��x�ĺ�����ϵʽ��
��2����������������4000Ԫ������Ӧ���ۼ۶�Ϊ����Ԫ��
��3���ò�Ʒÿǧ���ۼ�Ϊ����Ԫʱ�������̻�õ�����w��Ԫ�����ʱ���������Ϊ����Ԫ��


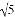 ��3_______0����������������������ţ�
��3_______0����������������������ţ�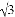 )2��9 B.
)2��9 B. 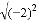 ����2
����2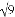 ����3 D.
����3 D. 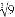 ����3
����3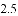
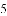
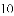
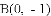
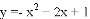 ��
��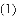
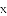
 ��ʵ���⣬��
��ʵ���⣬��