题目内容
已知图1和图2中，正方形的边长为1，按要求作格点三角形，并注相应的字母，
（1）在图1中作△ABC，使各其边长均为整数；
（2）在图2中作△A′B′C′，使△A′B′C′∽△ABC，并且A′B′：AB=
．
解：所作图形如下所示：
（1）作△ABC，使AC=3，AB=5，BC=4；
（2）∵△A′B′C′∽△ABC，并且A′B′：AB=，
∴两个三角形的相似比为，
作A'C'=3，
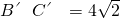，则A'B'=5．
分析：（1）可作△ABC，使AC=3，AB=5，BC=4；
（2）△A′B′C′∽△ABC，并且A′B′：AB=，即两个三角形的相似比为，可作A'C'=3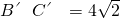，，则A'B'=5．
点评：本题考查了左图中的相似变换的知识，有一定难度，注意借助勾股定理使各边长均为整数．
（1）作△ABC，使AC=3，AB=5，BC=4；
（2）∵△A′B′C′∽△ABC，并且A′B′：AB=
，∴两个三角形的相似比为
，作A'C'=3
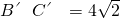，，则A'B'=5．分析：（1）可作△ABC，使AC=3，AB=5，BC=4；
（2）△A′B′C′∽△ABC，并且A′B′：AB=
，即两个三角形的相似比为，可作A'C'=3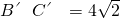，，则A'B'=5．点评：本题考查了左图中的相似变换的知识，有一定难度，注意借助勾股定理使各边长均为整数．
练习册系列答案
相关题目
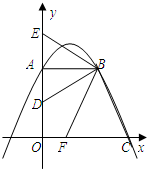边分别交y轴的正半轴、x轴的正半轴于点E和F．
（m≠
0）的图象相交于A、B两点，且A点的坐标是（1，2），B点的坐标是（-2，w）．
