题目内容
如图,已知在平面直角坐标系xOy中,直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两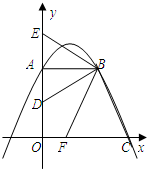 边分别交y轴的正半轴、x轴的正半轴于点E和F.
边分别交y轴的正半轴、x轴的正半轴于点E和F.(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ的周长最小,求出P、Q两点的坐标.
分析:(1)利用待定系数法代入求出二次函数解析式即可;
(2)利用配方法求出二次函数顶点坐标,再利用GH是△BEA的中位线.得出EA=3GH=
.进而得出CF=FM+CM得出答案;
(3)根据要使四边形BCPQ的周长最小,可将点C向上平移一个单位,再做关于对称轴对称的对称点C1,求出直线BC1的解析式,以及P、Q两点的坐标.
(2)利用配方法求出二次函数顶点坐标,再利用GH是△BEA的中位线.得出EA=3GH=
| 4 |
| 3 |
(3)根据要使四边形BCPQ的周长最小,可将点C向上平移一个单位,再做关于对称轴对称的对称点C1,求出直线BC1的解析式,以及P、Q两点的坐标.
解答: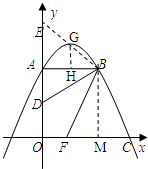 解:(1)由题意得A(0,2)、B(2,2)、C(3,0).
解:(1)由题意得A(0,2)、B(2,2)、C(3,0).
设经过A,B,C三点的抛物线的解析式为y=ax2+bx+2.
则
,
解得
,
∴y=-
x2+
x+2.
(2)由y=-
x2+
x+2=-
(x-1)2+
.
∴顶点坐标为G(1,
).
过G作GH⊥AB,垂足为H.
则AH=BH=1,GH=
-2=
.
∵EA⊥AB,GH⊥AB,
∴EA∥GH.
∴GH是△BEA的中位线.
∴EA=2GH=
.
过B作BM⊥OC,垂足为M.则MB=OA=AB.
∵∠EBF=∠ABM=90°,
∴∠EBA=∠FBM=90°-∠ABF.
∴Rt△EBA≌Rt△FBM.
∴FM=EA=
.
∵CM=OC-OM=3-2=1,
∴CF=FM+CM=
.
(3)要使四边形BCPQ的周长最小,
将B向下平移一个单位至K,取C关于对称轴对称点M.
连接KM交对称轴于P,将P向上平移1个单位至Q,
可使KP+PM最短.则QPKB为平行四边形,
QB=PK,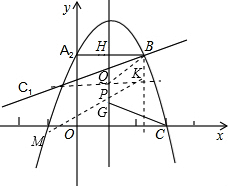
连接CP,轴对称求出CP=MP,
则CP+BQ最小,
因为CB,QP定值,则四边形BCPQ周长最短,
∵将点C向上平移一个单位,坐标为(3,1),再做关于对称轴对称的对称点C1,
∴得点C1的坐标为(-1,1).
可求出直线BC1的解析式为y=
x+
.
直线y=
x+
与对称轴x=1的交点即为点Q,坐标为Q(1,
).
∴点P的坐标为(1,
).
 解:(1)由题意得A(0,2)、B(2,2)、C(3,0).
解:(1)由题意得A(0,2)、B(2,2)、C(3,0).设经过A,B,C三点的抛物线的解析式为y=ax2+bx+2.
则
|
解得
|
∴y=-
| 2 |
| 3 |
| 4 |
| 3 |
(2)由y=-
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
∴顶点坐标为G(1,
| 8 |
| 3 |
过G作GH⊥AB,垂足为H.
则AH=BH=1,GH=
| 8 |
| 3 |
| 2 |
| 3 |
∵EA⊥AB,GH⊥AB,
∴EA∥GH.
∴GH是△BEA的中位线.
∴EA=2GH=
| 4 |
| 3 |
过B作BM⊥OC,垂足为M.则MB=OA=AB.
∵∠EBF=∠ABM=90°,
∴∠EBA=∠FBM=90°-∠ABF.
∴Rt△EBA≌Rt△FBM.
∴FM=EA=
| 4 |
| 3 |
∵CM=OC-OM=3-2=1,
∴CF=FM+CM=
| 7 |
| 3 |
(3)要使四边形BCPQ的周长最小,
将B向下平移一个单位至K,取C关于对称轴对称点M.
连接KM交对称轴于P,将P向上平移1个单位至Q,
可使KP+PM最短.则QPKB为平行四边形,
QB=PK,

连接CP,轴对称求出CP=MP,
则CP+BQ最小,
因为CB,QP定值,则四边形BCPQ周长最短,
∵将点C向上平移一个单位,坐标为(3,1),再做关于对称轴对称的对称点C1,
∴得点C1的坐标为(-1,1).
可求出直线BC1的解析式为y=
| 1 |
| 3 |
| 4 |
| 3 |
直线y=
| 1 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
∴点P的坐标为(1,
| 2 |
| 3 |
点评:此题主要考查了二次函数的综合题目,待定系数法求二次函数解析式以及利用三角形中位线的性质是解决问题的关键.

练习册系列答案
相关题目
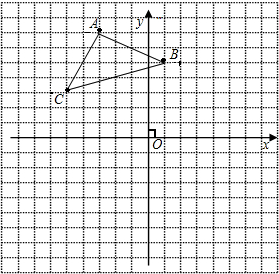 如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),
如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),
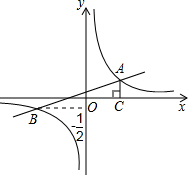 (2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=
(2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2= 如图,已知在平面直角坐标系中,△ABC的位置如图所示
如图,已知在平面直角坐标系中,△ABC的位置如图所示