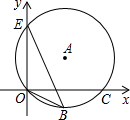题目内容
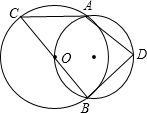
如图，AB，CD是⊙O的弦，AB⊥CD，BE是⊙O的直径．若AC=3，则DE=______．
连接AE，
∵BE是⊙O的直径，
∴∠BAE=90°，
即AB⊥AE，
∵AB⊥CD，
∴AE∥CD，
∴∠ACD+∠CAE=180°，
∵四边形ACDE是⊙O的内接四边形，
∴∠CAE+∠CDE=180°，
∴∠ACD=∠CDE，
∴
=
，
∴
=
，
∴DE=AC=3．
故答案为：3．
∵BE是⊙O的直径，
∴∠BAE=90°，
即AB⊥AE，
∵AB⊥CD，
∴AE∥CD，
∴∠ACD+∠CAE=180°，
∵四边形ACDE是⊙O的内接四边形，
∴∠CAE+∠CDE=180°，
∴∠ACD=∠CDE，
∴
 |
| CE |
|
| AD |
∴
|
| AC |
|
| DE |
∴DE=AC=3．
故答案为：3．
练习册系列答案
名校课堂系列答案
相关题目
-2，0），C（m，0），其中m＞0．以OB，OC为直径的圆分别交AB于点E，交AC于点F，连接EF．
