ΧβΡΩΡΎ»ί
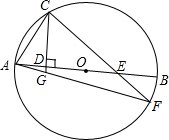
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷ΣΓςABCΒΡΕΞΒψΉχ±ξΖ÷±πΈΣAΘ®0Θ§3Θ©BΘ® -2Θ§0Θ©Θ§CΘ®mΘ§0Θ©Θ§Τδ÷–mΘΨ0Θ°“‘OBΘ§OCΈΣ÷±ΨΕΒΡ‘≤Ζ÷±πΫΜAB”ΎΒψEΘ§ΫΜAC”ΎΒψFΘ§Ν§Ϋ”EFΘ°
-2Θ§0Θ©Θ§CΘ®mΘ§0Θ©Θ§Τδ÷–mΘΨ0Θ°“‘OBΘ§OCΈΣ÷±ΨΕΒΡ‘≤Ζ÷±πΫΜAB”ΎΒψEΘ§ΫΜAC”ΎΒψFΘ§Ν§Ϋ”EFΘ°
Θ®1Θ©«σ÷ΛΘΚΓςAFEΓΉΓςABCΘΜ
Θ®2Θ© «Ζώ¥φ‘ΎmΒΡ÷ΒΘ§ ΙΒΟΓςAEF «Β»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«σ≥ωmΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©Ιέ≤λΒ±ΒψC‘Ύx÷α…œ“ΤΕ· ±Θ§ΒψF“ΤΕ·±δΜ·ΒΡ«ιΩωΘ° ‘«σΒψC1Θ®
Θ§0Θ©“ΤΕ·ΒΫΒψC2Θ®3
Θ§0Θ©ΒψF“ΤΕ·ΒΡ––≥ΧΘ°
 -2Θ§0Θ©Θ§CΘ®mΘ§0Θ©Θ§Τδ÷–mΘΨ0Θ°“‘OBΘ§OCΈΣ÷±ΨΕΒΡ‘≤Ζ÷±πΫΜAB”ΎΒψEΘ§ΫΜAC”ΎΒψFΘ§Ν§Ϋ”EFΘ°
-2Θ§0Θ©Θ§CΘ®mΘ§0Θ©Θ§Τδ÷–mΘΨ0Θ°“‘OBΘ§OCΈΣ÷±ΨΕΒΡ‘≤Ζ÷±πΫΜAB”ΎΒψEΘ§ΫΜAC”ΎΒψFΘ§Ν§Ϋ”EFΘ°Θ®1Θ©«σ÷ΛΘΚΓςAFEΓΉΓςABCΘΜ
Θ®2Θ© «Ζώ¥φ‘ΎmΒΡ÷ΒΘ§ ΙΒΟΓςAEF «Β»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«σ≥ωmΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©Ιέ≤λΒ±ΒψC‘Ύx÷α…œ“ΤΕ· ±Θ§ΒψF“ΤΕ·±δΜ·ΒΡ«ιΩωΘ° ‘«σΒψC1Θ®
| 3 |
| 3 |
Θ®1Θ©÷ΛΟςΘΚΓΏAO «ΝΫ‘≤ΡΎΒΡΙΪ«–œΏΘ§
ΓύAO2=AE•AB=AF•ACΘ§
Γύ
=
”÷ΓΏΓœFAE=ΓœBAC
ΓύΓςAFEΓΉΓςABCΘΜ
Θ®2Θ©ΓΏΓςAFEΓΉΓςABCΘ§
Γύ
=
=
Θ§
Β±AF=AEΘ§Φ¥AB=AC ±Θ§OC=OB
Γύm=2Θ§
Β±AE=FEΘ§Φ¥AB=BC ±Θ§
=2+mȧ
Γύm=
-2
Β±AF=FEΘ§Φ¥AC=BC ±Θ§9+m2=Θ®2+mΘ©2Θ§
ΫβΒΟm=
ΓύmΒΡ÷ΒΈΣ2Μρ
-2Μρ
ΘΜ
Θ®3Θ©ΓœAFO Φ÷’ΈΣ÷±Ϋ«Θ§«“OAΈΣΕ®÷Β
ΓύOA=3Θ§OC1=
Θ§
ΓύtanΓœOAC1=
Θ§
ΓύΓœOAC1=30ΓψΘ§
Ά§άμΩ…ΒΟΓœOAC2=60Γψ
ΓύΓœC1AC2=30Γψ
ΓύΒψF“ΤΕ·ΒΡ––≥ΧΈΣ
=
Θ°
ΓύAO2=AE•AB=AF•ACΘ§
Γύ
| AE |
| AF |
| AC |
| AB |
”÷ΓΏΓœFAE=ΓœBAC
ΓύΓςAFEΓΉΓςABCΘΜ
Θ®2Θ©ΓΏΓςAFEΓΉΓςABCΘ§
Γύ
| AF |
| AB |
| AE |
| AC |
| FE |
| BC |
Β±AF=AEΘ§Φ¥AB=AC ±Θ§OC=OB
Γύm=2Θ§
Β±AE=FEΘ§Φ¥AB=BC ±Θ§
| 4+9 |
Γύm=
| 13 |
Β±AF=FEΘ§Φ¥AC=BC ±Θ§9+m2=Θ®2+mΘ©2Θ§
ΫβΒΟm=
| 5 |
| 4 |
ΓύmΒΡ÷ΒΈΣ2Μρ
| 13 |
| 5 |
| 4 |
Θ®3Θ©ΓœAFO Φ÷’ΈΣ÷±Ϋ«Θ§«“OAΈΣΕ®÷Β
ΓύOA=3Θ§OC1=
| 3 |
ΓύtanΓœOAC1=
| ||
| 3 |
ΓύΓœOAC1=30ΓψΘ§
Ά§άμΩ…ΒΟΓœOAC2=60Γψ
ΓύΓœC1AC2=30Γψ
ΓύΒψF“ΤΕ·ΒΡ––≥ΧΈΣ
(2ΓΝ30)ΓΝΠ–ΓΝ
| ||
| 180 |
| Π– |
| 2 |

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ