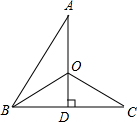题目内容
如图，△ABC和△ADE都是等腰三角形，且∠BAC=90°，∠DAE=90°，B，C，D
在同一条直线上．求证：BD=CE．
在同一条直线上．求证：BD=CE．
证明：∵△ABC和△ADE都是等腰直角三角形，
∴AD=AE，AB=AC。
又∵∠EAC=90°+∠CAD，∠DAB=90°+∠CAD，∴∠DAB=∠EAC。
∵在△ADB和△AEC中，
，
∴△ADB≌△AEC（SAS）。∴BD=CE。
∴AD=AE，AB=AC。
又∵∠EAC=90°+∠CAD，∠DAB=90°+∠CAD，∴∠DAB=∠EAC。
∵在△ADB和△AEC中，
，∴△ADB≌△AEC（SAS）。∴BD=CE。
试题分析：求出AD=AE，AB=AC，∠DAB=∠EAC，根据SAS证出△ADB≌△AEC即可。
练习册系列答案
相关题目
，CP
，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是
