题目内容
如果a、b、c分别是△ABC三边的长，且|a+b-c|+|b+c-a|+|c+a-b|=12，那么△ABC的周长是 ．
考点：三角形三边关系
专题：
分析：先根据三角形三边关系定理及绝对值的定义化简已知等式的左边，再合并同类项即可求解．
解答：解：∵a、b、c分别是△ABC三边的长，
∴a+b-c＞0，b+c-a＞0，c+a-b＞0．
∵|a+b-c|+|b+c-a|+|c+a-b|=12，
∴a+b-c+b+c-a+c+a-b=12，
∴a+b+c=12，
即△ABC的周长是12．
故答案为12．
∴a+b-c＞0，b+c-a＞0，c+a-b＞0．
∵|a+b-c|+|b+c-a|+|c+a-b|=12，
∴a+b-c+b+c-a+c+a-b=12，
∴a+b+c=12，
即△ABC的周长是12．
故答案为12．
点评：本题考查了三角形三边关系定理：三角形两边之和大于第三边．同时考查了绝对值的定义．
练习册系列答案
相关题目
如果直线y=kx+b经过一、二、四象限，则有（ ）
| A、k＞0，b＞0 |
| B、k＞0，b＜0 |
| C、k＜0，b＞0 |
| D、k＜0，b＜0 |
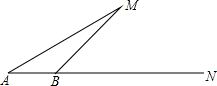有一次，小明坐着轮船由A点出发沿正东方向AN航行，在A点望湖中小岛M，测得∠MAN=30°，航行100米到达B点时，测得∠MBN=45°，你能算出A点与湖中小岛M的距离吗？