题目内容
如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连结BE交AC于F,连结FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD②△FED与△DEB③△CFD与△ABG④△ADF与△CFB中相似的为( )
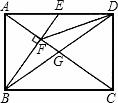
A.①④ B.①② C.②③④ D.①②③
D.
【解析】根据题意得:∠BAE=∠ADC=∠AFE=90°,∴∠AEF+∠EAF=90°,∠DAC+∠ACD=90°,∴∠AEF=∠ACD,∴①中两三角形相似; 容易判断△AFE∽△BAE,得 ,
,
又∵AE=ED,∴ 而∠BED=∠BED,∴△FED∽△DEB.故②正确;
而∠BED=∠BED,∴△FED∽△DEB.故②正确;
∵AB∥CD,∴∠BAC=∠GCD,∵∠ABE=∠DAF,∠EBD=∠EDF,且∠ABG=∠ABE+∠EBD,
∴∠ABG=∠DAF+∠EDF=∠DFC;∵∠ABG=∠DFC,∠BAG=∠DCF,∴△CFD∽△ABG,故③正确;所以相似的有①②③.
故选D.

练习册系列答案
相关题目

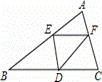

 中,
中, ,以点
,以点 为圆心,
为圆心, 为半径的圆弧交
为半径的圆弧交 于点
于点 ,交
,交 的延长线于点
的延长线于点 ,
,
 则图中阴影部分的面积为 .(结果保留
则图中阴影部分的面积为 .(结果保留 )
)
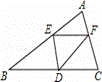

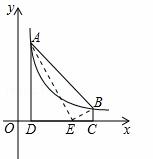

 ____.(只需写出一个)
____.(只需写出一个)