题目内容
如图,小岛A在港口P的南偏西4 5°方向,距离港口81海里处,甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口.现两船同时出发.
5°方向,距离港口81海里处,甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口.现两船同时出发.
(1)出发后几小时两船与港口P的距离相等?
(2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)(参考数据: ≈1.41,
≈1.41,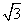 ≈1.73)
≈1.73)

解:(1)设出发后xh两船与港口P的距离相等,
根据题意,得81-9x=18x,解这个方程,得x=3,
∴出发后3h两船与港口P的距离相等.
(2)设出发后xh乙船在甲船的正东方向,
此时甲、乙两船的 位置分别在点C,D处,
位置分别在点C,D处,
连接CD,过点P作PE⊥CD,垂足为E,则点E在点P的正南方向.
在Rt△CEP中,∠CPE=45°,
 ∴PE=PC·cos45°,
∴PE=PC·cos45°,
在Rt△PED中,∠EPD=6 0
0 °
°
∴PE=PD·cos60°,
∴PC·cos45°=PD·cos60°,
∴(81-9x)·cos45°=18x·cos60°,
解这个方程,得x≈3.7,
∴出发后约3.7h乙船在甲船的正东方向.

练习册系列答案
相关题目
 中,当x>0时,y随x的增大而增大,则二次函数
中,当x>0时,y随x的增大而增大,则二次函数 图像大致是( )
图像大致是( )
 .6海里内有暗礁,问这条渔船按原来的方向续航行,有没有触礁的危
.6海里内有暗礁,问这条渔船按原来的方向续航行,有没有触礁的危 险?
险?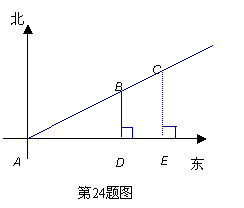
 =cos
=cos ;③
;③ =tanB,其中正确的结论是______.(填序号)
=tanB,其中正确的结论是______.(填序号) <cosA<
<cosA<
 D.
D. 知AC=
知AC=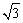 ,BC=
,BC=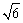 ,AB=3,那么sin A=_______.
,AB=3,那么sin A=_______. 的值 ( )
的值 ( ) 1
1 ;
;