题目内容
如图，半径为5的⊙P与y轴相交于M（0，-3），N（0，-11）两点，则P到原点O的距离OP的长为（ ）| A、6 | ||
| B、7 | ||
C、
| ||
| D、8 |
分析：先根据M、N两点的坐标求出MN、ON的值，再连接PN，过P作PA⊥y轴于A，由垂径定理可求出AN的值，再由勾股定理即可求出OP的值．
解答：
解：∵M（0，-3），N（0，-11），
∴MN=|-11+3|=8，
∴ON=11，
连接PN，过P作PA⊥y轴于A，
则AN=
MN=
×8=4，
∴OA=11-4=7，
在Rt△PAN中，PN=5，AN=4，
∴PA=3，
在Rt△OPA中，
OP=
=
=
．
故选C．
解：∵M（0，-3），N（0，-11），∴MN=|-11+3|=8，
∴ON=11，
连接PN，过P作PA⊥y轴于A，
则AN=
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=11-4=7，
在Rt△PAN中，PN=5，AN=4，
∴PA=3，
在Rt△OPA中，
OP=
| PA2+OA2 |
| 32+72 |
| 58 |
故选C．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线是解答此题的关键．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
如图，半径为1的⊙D内切于圆心角为60°的扇形OAB，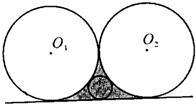
12、如图，半径为4的两等圆相外切，它们的一条外公切线与两圆围成的阴影部分中，存在的最大圆的半径等于
如图，半径为30km 的圆A是环保部分划定的生态保护区，B、C是位于保护区附近相距100km的两城市．如果在 B、C两城之间修一条笔直的公路，经测量∠ABC=45°，∠ACB=30°．
如图，半径为1的小圆在半径为9的大圆内滚动，且始终与大圆相切，则小圆扫过的阴影部分的面积为
（2013•高淳县一模）如图，半径为2的两个等圆⊙O1与⊙O2外切于点P，过O1作⊙O2的两条切线，切点分别为A、B，与⊙O1分别交于C、D，则弧APB与弧CPD的长度之和为