题目内容
4.已知两个相似三角形的相似比是4:9,那么它们对应的角平分线之比是4:9.分析 直接根据相似三角形的性质即可得出结论.
解答 解:∵两个相似三角形的相似比是4:9,
∴它们对应的角平分线之比是4:9.
故答案为:4:9.
点评 本题考查的是相似三角形的性质,熟知相似三角形对应角平分线的比等于相似比是解答此题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
12.下列命题是真命题的是( )
| A. | 若直线y=-kx-2过第一、三、四象限,则k<0 | |
| B. | 三角形三条角平分线的交点到三个顶点的距离相等 | |
| C. | 如果∠A=∠B,那么∠A和∠B是对顶角 | |
| D. | 如果a•b=0,那么a=0 |
19.已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中正确的是( )
| A. | sinA=$\frac{2}{3}$ | B. | cosA=$\frac{2}{3}$ | C. | tanA=$\frac{2}{3}$ | D. | cotA=$\frac{2}{3}$ |
16.某商品降低x%后是a元,则原价是( )
| A. | a•x%元 | B. | a(1+x%)元 | C. | $\frac{a}{x%}$元 | D. | $\frac{a}{1-x%}$元 |
14.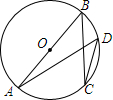 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )| A. | $\frac{{8\sqrt{13}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{{24\sqrt{5}}}{5}$ | D. | 12 |
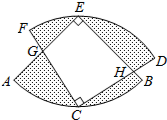 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点,若扇形的半径为$\sqrt{2}$,则图中阴影部分的面积等于π-2.
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点,若扇形的半径为$\sqrt{2}$,则图中阴影部分的面积等于π-2. 如图,已知在△ABC中,AD是BC边的中线,AE=EF=CF,BE与AD交于点G,求DF:GB的值.
如图,已知在△ABC中,AD是BC边的中线,AE=EF=CF,BE与AD交于点G,求DF:GB的值.