题目内容
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
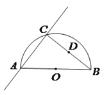
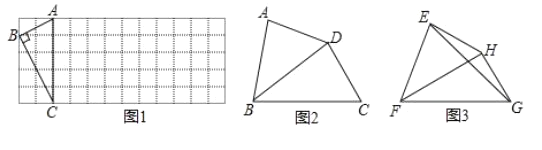
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点 D,使四边形ABCD是以AC为“相似对角线”的四边形(画出1个即可);
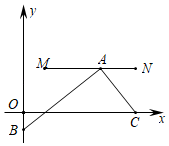
(2)如图2,在四边形ABCD中,![]() ,对角线BD平分∠ABC.
,对角线BD平分∠ABC.
求证: BD是四边形ABCD的“相似对角线”;
运用:
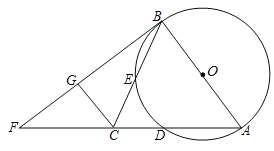
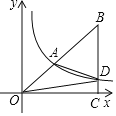
(3)如图3,已知FH是四边形EFGH的“相似对角线”,∠EFH=∠HFG=![]() .连接EG,若△EFG的面积为
.连接EG,若△EFG的面积为![]() ,求FH的长.
,求FH的长.
【答案】(1)详见解析;(2)详见解析;(3)4
【解析】
(1)根据“相似对角线”的定义,利用方格纸的特点可找到D点的位置.
(2)通过导出对应角相等证出![]() ∽
∽![]() ,根据四边形ABCD的“相似对角线”的定义即可得出BD是四边形ABCD的“相似对角线”.
,根据四边形ABCD的“相似对角线”的定义即可得出BD是四边形ABCD的“相似对角线”.
(3)根据四边形“相似对角线”的定义,得出![]() ∽
∽![]() ,利用对应边成比例,结合三角形面积公式即可求.
,利用对应边成比例,结合三角形面积公式即可求.
解:(1)如图1所示.



(2)证明:
![]() 平分
平分![]() ,
,
![]()

![]() ∽
∽![]()
∴BD是四边形![]() 的“相似对角线”.
的“相似对角线”.
(3)![]() 是四边形
是四边形![]() 的“相似对角线”,
的“相似对角线”,
![]() 三角形
三角形![]() 与三角形
与三角形![]() 相似.
相似.
又![]()
![]() ∽
∽![]()
![]()
![]()
过点![]() 作
作![]() 垂足为
垂足为![]()
则![]()

![]()
![]()
![]()
![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】如图,已知△AOB与△A1OB1是以点O为位似中心的位似图形,且相似比为1:2,点B的坐标为(-1,2),则点B1的坐标为( )
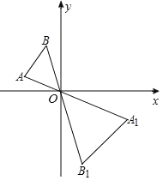
A.(2,-4)B.(1,-4)C.(-1,4)D.(-4,2)