题目内容
设x,y是大于零的实数,且 ,则
,则 =________.
=________.
4
分析:根据比例的性质由 =
= 得
得 =
= ,由三角函数的关系有
,由三角函数的关系有 =tanθ,则tanθ=
=tanθ,则tanθ= ,在△ABC中,∠C=90°,AC=x,BC=y,根据锐角三角函数的定义得到
,在△ABC中,∠C=90°,AC=x,BC=y,根据锐角三角函数的定义得到
sinθ= ,cosθ=
,cosθ= ,则
,则 +
+ =
= 可化为
可化为 •
• +
+ •
• =
= ,化简后得
,化简后得 +
+ =14,配方后得到(
=14,配方后得到( +
+ )2=16,然后两边开方取算术平方根即可.
)2=16,然后两边开方取算术平方根即可.
解答:∵ =
= ,
,
∴ =
= ,而
,而 =tanθ,
=tanθ,
∴tanθ= ,
,
如图,在△ABC中,∠C=90°,AC=x,BC=y,
∴AB= ,
,
∴sinθ= ,cosθ=
,cosθ= ,
,
而 +
+ =
= ,
,
∴ •
• +
+ •
• =
= ,
,
∴ +
+ =14,
=14,
∴( +
+ )2-2=14,
)2-2=14,
∴( +
+ )2=16,
)2=16,
而x,y是大于零的实数,
∴ +
+ =4.
=4.
故答案为4.
点评:本题考查了锐角三角函数的定义:在直角三角形中,一锐角的正弦等于它的对边与斜边的比值;一锐角的余弦等于它的邻边与斜边的比值;一锐角的正切等于它的对边与它的邻边的比值.也考查了勾股定理、完全平方公式以及比例的性质.
分析:根据比例的性质由
 =
= 得
得 =
= ,由三角函数的关系有
,由三角函数的关系有 =tanθ,则tanθ=
=tanθ,则tanθ= ,在△ABC中,∠C=90°,AC=x,BC=y,根据锐角三角函数的定义得到
,在△ABC中,∠C=90°,AC=x,BC=y,根据锐角三角函数的定义得到sinθ=
 ,cosθ=
,cosθ= ,则
,则 +
+ =
= 可化为
可化为 •
• +
+ •
• =
= ,化简后得
,化简后得 +
+ =14,配方后得到(
=14,配方后得到( +
+ )2=16,然后两边开方取算术平方根即可.
)2=16,然后两边开方取算术平方根即可.解答:∵
 =
= ,
,
∴
 =
= ,而
,而 =tanθ,
=tanθ,∴tanθ=
 ,
,如图,在△ABC中,∠C=90°,AC=x,BC=y,
∴AB=
 ,
,∴sinθ=
 ,cosθ=
,cosθ= ,
,而
 +
+ =
= ,
,∴
 •
• +
+ •
• =
= ,
,∴
 +
+ =14,
=14,∴(
 +
+ )2-2=14,
)2-2=14,∴(
 +
+ )2=16,
)2=16,而x,y是大于零的实数,
∴
 +
+ =4.
=4.故答案为4.
点评:本题考查了锐角三角函数的定义:在直角三角形中,一锐角的正弦等于它的对边与斜边的比值;一锐角的余弦等于它的邻边与斜边的比值;一锐角的正切等于它的对边与它的邻边的比值.也考查了勾股定理、完全平方公式以及比例的性质.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
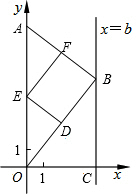 如图,在直角坐标系中,点A的坐标为(0,8),点 B(b,t)在直线x=b上运动,点D、E、F分别为OB、0A、AB的中点,其中b是大于零的常数.
如图,在直角坐标系中,点A的坐标为(0,8),点 B(b,t)在直线x=b上运动,点D、E、F分别为OB、0A、AB的中点,其中b是大于零的常数.