题目内容
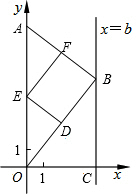 如图,在直角坐标系中,点A的坐标为(0,8),点 B(b,t)在直线x=b上运动,点D、E、F分别为OB、0A、AB的中点,其中b是大于零的常数.
如图,在直角坐标系中,点A的坐标为(0,8),点 B(b,t)在直线x=b上运动,点D、E、F分别为OB、0A、AB的中点,其中b是大于零的常数.(1)判断四边形DEFB的形状.并证明你的结论;
(2)试求四边形DEFB的面积S与b的关系式;
(3)设直线x=b与x轴交于点C,问:四边形DEFB能不能是矩形?若能.求出t的值;若不能,说明理由.
分析:(1)四边形DEFB是平行四边形.利用DE、EF为△OAB的中位线证明平行四边形;
(2)根据DE、EF为△OAB的中位线可知,S△AEF=S△ODE=
S△AOB,利用S=S△AOB-S△AEF-S△ODE求S与b的关系式;
(3)当∠ABO=90°时,四边形DEFB是矩形,由Rt△OCB∽Rt△ABO,根据相似比得OB2=OA•BC,由勾股定理得OB2=BC2+OC2,利用b、t分别表示线段的长,列方程求解.
(2)根据DE、EF为△OAB的中位线可知,S△AEF=S△ODE=
| 1 |
| 4 |
(3)当∠ABO=90°时,四边形DEFB是矩形,由Rt△OCB∽Rt△ABO,根据相似比得OB2=OA•BC,由勾股定理得OB2=BC2+OC2,利用b、t分别表示线段的长,列方程求解.
解答:解:(1)四边形DEFB是平行四边形.
证明:∵D、E分别是OB、OA的中点,
∴DE∥AB,同理,EF∥OB,
∴四边形DEFB是平行四边形;
(2)解法一:∵S△AOB=
×8×b=4b,
由(1)得EF∥OB,∴△AEF∽△AOB,
∴
=(
)2,即S△AEF=
S△AOB=b,同理S△ODE=b,
∴S=S△AOB-S△AEF-S△ODE=4b-b-b=2b,即S=2b(b>0);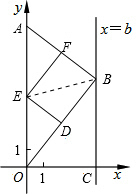
解法二:如图,连接BE,S△AOB=
×8×b=4b,
∵E、F分别为OA、AB的中点,
∴S△AEF=
S△AEB=
S△AOB=b,
同理S△EOD=b,
∴S=S△AOB-S△AEF-S△ODE=4b-b-b=2b,
即S=2b(b>0);
(3)解法一:以E为圆心,OA长为直径的圆记为⊙E,
①当直线x=b与⊙E相切或相交时,若点B是切点或交点,则∠ABO=90°,由(1)知,四边形DEFB是矩形,
此时0<b≤4,可得△AOB∽△OBC,
∴
=
,即OB2=OA•BC=8t,
在Rt△OBC中,OB2=BC2+OC2=t2+b2,
∴t2+b2=8t,
∴t2-8t+b2=0,
解得t=4±
,
②当直线x=b与⊙E相离时,∠ABO≠90°,
∴四边形DEFB不是矩形,
综上所述:当0<b≤4时,四边形DEFB是矩形,这时,t=4±
,当b>4时,四边形DEFB不是矩形;
解法二:由(1)知,当∠ABO=90°时,四边形DEFB是矩形,
∵∠COB+∠AOB=90°,∠OAB+∠AOB=90°,
∴∠COB=∠OAB,
又∵∠ABO=∠OCB=90°,
∴Rt△OCB∽Rt△ABO,
∴
=
,即OB2=OA•BC,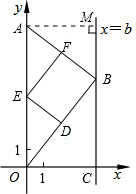
又OB2=BC2+OC2=t2+b2,OA=8,BC=t(t>0),
∴t2+b2=8t,
∴(t-4)2=16-b2,
①当16-b2≥0时,解得t=4±
,此时四边形DEFB是矩形,
②当16-b2<0时,t无实数解,此时四边形DEFB不是矩形,
综上所述:当16-b2≥0时,四边形DEFB是矩形,此时t=4±
,当16-b2<0时,四边形DEFB不是矩形;
解法三:如图,过点A作AM⊥BC,垂足为M,
在Rt△AMB中,AB2=AM2+BM2=b2+(8-t)2,
在Rt△OCB中,OB2=OC2+BC2=b2+t2,
在△OAB中,当AB2+OB2=OA2时,∠ABO=90°,则四边形DEFB为矩形,
∴b2+(8-t)2+b2+t2=82,
化简得t2-8t=-b2,配方得(t-4)2=16-b2,其余同解法二.
证明:∵D、E分别是OB、OA的中点,
∴DE∥AB,同理,EF∥OB,
∴四边形DEFB是平行四边形;
(2)解法一:∵S△AOB=
| 1 |
| 2 |
由(1)得EF∥OB,∴△AEF∽△AOB,
∴
| S△AEF |
| S△AOB |
| 1 |
| 2 |
| 1 |
| 4 |
∴S=S△AOB-S△AEF-S△ODE=4b-b-b=2b,即S=2b(b>0);

解法二:如图,连接BE,S△AOB=
| 1 |
| 2 |
∵E、F分别为OA、AB的中点,
∴S△AEF=
| 1 |
| 2 |
| 1 |
| 4 |
同理S△EOD=b,
∴S=S△AOB-S△AEF-S△ODE=4b-b-b=2b,
即S=2b(b>0);
(3)解法一:以E为圆心,OA长为直径的圆记为⊙E,
①当直线x=b与⊙E相切或相交时,若点B是切点或交点,则∠ABO=90°,由(1)知,四边形DEFB是矩形,
此时0<b≤4,可得△AOB∽△OBC,
∴
| OB |
| BC |
| OA |
| BO |
在Rt△OBC中,OB2=BC2+OC2=t2+b2,
∴t2+b2=8t,
∴t2-8t+b2=0,
解得t=4±
| 16-b2 |
②当直线x=b与⊙E相离时,∠ABO≠90°,
∴四边形DEFB不是矩形,
综上所述:当0<b≤4时,四边形DEFB是矩形,这时,t=4±
| 16-b2 |
解法二:由(1)知,当∠ABO=90°时,四边形DEFB是矩形,
∵∠COB+∠AOB=90°,∠OAB+∠AOB=90°,
∴∠COB=∠OAB,
又∵∠ABO=∠OCB=90°,
∴Rt△OCB∽Rt△ABO,
∴
| BC |
| OB |
| OB |
| AO |

又OB2=BC2+OC2=t2+b2,OA=8,BC=t(t>0),
∴t2+b2=8t,
∴(t-4)2=16-b2,
①当16-b2≥0时,解得t=4±
| 16-b2 |
②当16-b2<0时,t无实数解,此时四边形DEFB不是矩形,
综上所述:当16-b2≥0时,四边形DEFB是矩形,此时t=4±
| 16-b2 |
解法三:如图,过点A作AM⊥BC,垂足为M,
在Rt△AMB中,AB2=AM2+BM2=b2+(8-t)2,
在Rt△OCB中,OB2=OC2+BC2=b2+t2,
在△OAB中,当AB2+OB2=OA2时,∠ABO=90°,则四边形DEFB为矩形,
∴b2+(8-t)2+b2+t2=82,
化简得t2-8t=-b2,配方得(t-4)2=16-b2,其余同解法二.
点评:本题考查了平行四边形、矩形、相似三角形的判定与性质,一次函数及勾股定理的运用.本题综合性较强,需要熟练掌握特殊图形的性质,形数结合,运用代数方法解答几何问题.

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: