题目内容
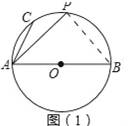
如图,AB是⊙O的直径,C,P是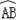
 上两点,AB=13,AC=5.
上两点,AB=13,AC=5.
(1)如图(1),若点P是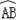
 的中点,求PA的长;
的中点,求PA的长;
(2)如图(2),若点P是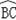
 的中点,求PA的长.
的中点,求PA的长.
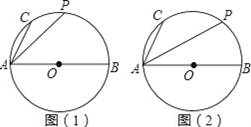

【考点】相似三角形的判定与性质;勾股定理;等腰直角三角形;圆心角、弧、弦的关系;圆周角定理.
【专题】几何综合题.
【分析】(1)根据圆周角的定理,∠APB=90°,P是弧AB的中点,所以三角形APB是等腰三角形,利用勾股定理即可求得.
(2)根据垂径定理得出OP垂直平分BC,得出OP∥AC,从而得出△ACB∽△0NP,根据对应边成比例求得ON、AN的长,利用勾股定理求得NP的长,进而求得PA.
【解答】解:(1)如图(1)所示,连接PB,

∵AB是⊙O的直径且P是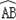
 的中点,
的中点,
∴∠PAB=∠PBA=45°,∠APB=90°,
又∵在等腰三角形△APB中有AB=13,
∴PA=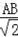
 =
=
 =
=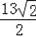
 .
.
(2)如图(2)所示:连接BC.OP相交于M点,作PN⊥AB于点N,


∵P点为弧BC的中点,
∴OP⊥BC,∠OMB=90°,
又因为AB为直径
∴∠ACB=90°,
∴∠ACB=∠OMB,
∴OP∥AC,
∴∠CAB=∠POB,
又因为∠ACB=∠ONP=90°,
∴△ACB∽△0NP
∴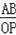
 =
=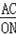
 ,
,
又∵AB=13 AC=5 OP=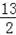
 ,
,
代入得 ON=
 ,
,
∴AN=OA+ON=9
∴在Rt△OPN中,有NP2=0P2﹣ON2=36
在Rt△ANP中 有PA=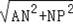
 =
=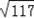
 =3
=3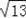

∴PA=3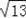
 .
.
【点评】本题考查了圆周角的定理,垂径定理,勾股定理,等腰三角形判定和性质,相似三角形的判定和性质,作出辅助线是本题的关键.

练习册系列答案
相关题目
 与a之间的关系.
与a之间的关系.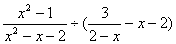 ,再从-2,-1,0,1,四个数中选取一
,再从-2,-1,0,1,四个数中选取一 个适当的数作为
个适当的数作为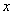 的值代入求值.
的值代入求值.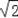
 C.1,1,
C.1,1,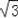

 ,求代数式(
,求代数式(
 +2)÷
+2)÷
 .
.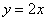 的图像与反比例函数
的图像与反比例函数 的图像没有交点,则实数
的图像没有交点,则实数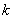 的取值范围在数轴上可表示为 ( )
的取值范围在数轴上可表示为 ( )
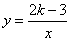 ,当
,当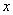 <0时,
<0时,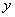 随
随