题目内容
14. 如图,平行四边形ABCD中,AE⊥BD于E,且BE:DE=3:7,BD=20,AB=10,则AB,CD的距离为16.
如图,平行四边形ABCD中,AE⊥BD于E,且BE:DE=3:7,BD=20,AB=10,则AB,CD的距离为16.
分析 由BE:DE=3:7,BD=20,可求得BE的长,然后利用勾股定理,求得AE的长,继而可求得?ABCD的面积,则可求得AB,CD的距离.
解答 解:BE:DE=3:7,BD=20,
∴BE=$\frac{3}{3+7}$×20=6,
∵AE⊥BD,AB=10,
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=8,
∴S?ABCD=2S△ABD=2×$\frac{1}{2}$×20×8=160,
∴AB,CD的距离为:160÷10=16.
故答案为:16.
点评 此题考查了平行四边形的性质以及勾股定理.注意利用面积求解是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.用围棋子按下面的规律摆图形,则摆第2012个图形需要围棋子的枚数是( )


| A. | 6035 | B. | 6038 | C. | 6041 | D. | 6044 |
19.平行四边形的两条对角线长分别为8和10,则其中每一边长x的取值范围是( )
| A. | 2<x<18 | B. | 1<x<9 | C. | 0<x<10 | D. | 0<x<8 |
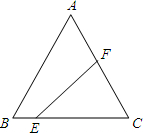 在△ABC中,AB=AC=5,BC=6.若点E在BC上运动(E与B、C不重合),点F在CA上运动,且EF平分△ABC的周长,设CE=x,△CEF的面积为y.
在△ABC中,AB=AC=5,BC=6.若点E在BC上运动(E与B、C不重合),点F在CA上运动,且EF平分△ABC的周长,设CE=x,△CEF的面积为y.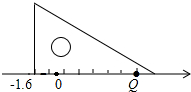 慧慧自己做了一个三角形的纸片,并在其中的一边画了七个长度相等的小格,每小格的长度为1个单位长度,然后把此边放在如图所示的数轴上,则点Q所表示的数是5.4.
慧慧自己做了一个三角形的纸片,并在其中的一边画了七个长度相等的小格,每小格的长度为1个单位长度,然后把此边放在如图所示的数轴上,则点Q所表示的数是5.4.