题目内容
如图,已知:△ABC和△ADE均为等边三角形,点D在BC边上,DE与AC交于点F.
(1)写出图中的相似三角形;
 (2)求证:AE2=AF·AC.
(2)求证:AE2=AF·AC.
(1)△ABC∽△ADE
 △ABD∽△AEF
△ABD∽△AEF
△ABD∽△DCF
△AEF∽△DCF
△ADF∽△ACD
答对一个得一分,答错一个扣一分,本问得分为对得分减去错扣分,结果为负数记零分,满分5分。
(2)证明:∵△ABC和△ADE均为等边三角形
∴∠B=∠E=60°,∠BAC=∠EAD=60°,AB=AC,AD=AE------------------------------------7
∴∠BAD=∠EAF=60°-∠DAF----------------------------------------------8
∴△ABD∽△AEF-----------------------------------------------------------9

∴ --------------------------------------------------------------------------10
∴AB·AF =AE·AD
∴AC·AF =AE·AE--------------------------------------------------------------------11
∴AE2=AF·AC-----------------------------------------------------------------------12

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
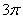 B.
B. C.
C. D.
D.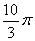
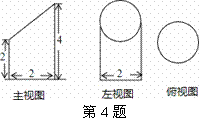
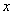 的一元二次方程
的一元二次方程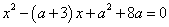 的两个实数根分别为4和
的两个实数根分别为4和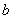 ,求
,求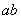 的值.
的值.

 .
.