题目内容
18.(1)计算:2-1-$\sqrt{3}$tan60°+(π-2016)0+|-$\frac{1}{2}$|(2)化简:(x+$\frac{1}{x}$-$\frac{x}{x-1}$)÷$\frac{1}{(x-1)^{2}}$.
分析 (1)根据负整数指数幂、零指数幂、特殊角的三角函数值、绝对值的定义化简即可.
(2)先计算括号后计算除法即可.
解答 解:(1)2-1-$\sqrt{3}$tan60°+(π-2016)0+|-$\frac{1}{2}$|
=$\frac{1}{2}$-$\sqrt{3}$×$\sqrt{3}$+1+$\frac{1}{2}$
=$\frac{1}{2}$-3+$\frac{3}{2}$
=-1;
(2)(x+$\frac{1}{x}$-$\frac{x}{x-1}$)÷$\frac{1}{(x-1)^{2}}$.
=$\frac{{x}^{2}(x-1)+(x-1)-{x}^{2}}{x(x-1)}$•(x-1)2
=$\frac{{x}^{4}-3{x}^{3}+3{x}^{2}-2x+1}{x}$
点评 本题考查负整数指数幂、零指数幂、特殊角的三角函数值、绝对值的定义等性质,记住这些定义是解决问题的关键,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.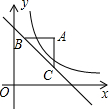 如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点,若函数y=$\frac{k}{x}$(x>0)的图象△ABC的边有公共点,则k的取值范围是( )
如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点,若函数y=$\frac{k}{x}$(x>0)的图象△ABC的边有公共点,则k的取值范围是( )
 如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点,若函数y=$\frac{k}{x}$(x>0)的图象△ABC的边有公共点,则k的取值范围是( )
如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点,若函数y=$\frac{k}{x}$(x>0)的图象△ABC的边有公共点,则k的取值范围是( )| A. | 5≤k≤20 | B. | 8≤k≤20 | C. | 5≤k≤8 | D. | 9≤k≤20 |
6.为了解某班学生每天使用零花钱的情况,小明随机查了15名同学,结果如下表:
关于这15名同学每天使用的零花钱,下列说法正确的是( )
| 每天使用零花钱(单位:元) | 0 | 1 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 5 | 4 | 2 |
| A. | 众数是5元 | B. | 极差是4元 | C. | 中位数3元 | D. | 平均数是2.5元 |
7.甲、乙二人在相同条件下各射靶10次,每次射靶成绩如图所示,经计算得:$\overline{{x}_{甲}}$-$\overline{{x}_{乙}}$=1,S${\;}_{甲}^{2}$=1.2,S${\;}_{乙}^{2}$=5.8,则下列结论中不正确的是( )
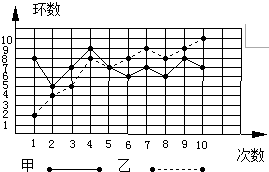

| A. | 甲、乙的总环数相等 | B. | 甲的成绩稳定 | ||
| C. | 甲、乙的众数相同 | D. | 乙的发展潜力更大 |
8.下列各数中最小的是( )
| A. | -π | B. | -3 | C. | -$\sqrt{5}$ | D. | 0 |
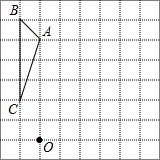 如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,请完成下列任务:
如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,请完成下列任务: 如图所示的几何体是由五个大小相同的正方体搭建而成的,它的左视图是( )
如图所示的几何体是由五个大小相同的正方体搭建而成的,它的左视图是( )


