题目内容
在锐角△ABC中,AB=8,BC=6,∠ACB=60°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为12,求△CBC1的面积;
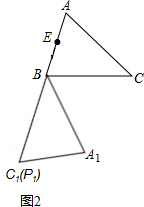
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,则线段EP1长度的最大值是 ,最小值是 .
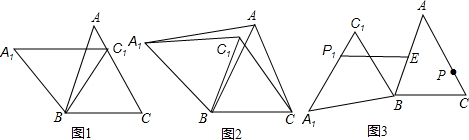
(1)如图1,当点C1在线段CA上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为12,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,则线段EP1长度的最大值是

考点:旋转的性质
专题:
分析:(1)由由旋转的性质可得:∠A1C1B=∠ACB=60°,BC=BC1,又由等腰三角形的性质,即可求得∠CC1A1的度数;
(2)由△ABC≌△A1BC1,易证得△ABA1∽△CBC1,然后利用相似三角形的面积比等于相似比的平方,即可求得△CBC1的面积;
(3)由①当P在AC上运动至垂足点D,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小;②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,即可求得线段EP1长度的最大值与最小值.
(2)由△ABC≌△A1BC1,易证得△ABA1∽△CBC1,然后利用相似三角形的面积比等于相似比的平方,即可求得△CBC1的面积;
(3)由①当P在AC上运动至垂足点D,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小;②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,即可求得线段EP1长度的最大值与最小值.
解答:解:(1)由旋转的性质可得:∠A1C1B=∠ACB=60°,BC=BC1,
∴∠CC1B=∠C1CB=60°,
∴∠CC1A1=∠CC1B+∠A1C1B=60°+60°=120°.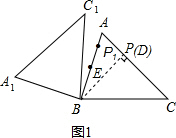
(2)∵△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴
=
,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
∴∠ABA1=∠CBC1,
∴△ABA1∽△CBC1.
∴
=(
)2=(
)2=
,
∵S△ABA1=12,
∴S△CBC1=
;
(3)①如图1,过点B作BD⊥AC,D为垂足,
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin60°=6×
=3
,
当P在AC上运动,BP与AC垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1-BE=BD-BE=3
-4;
②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BC+BE=6+4=10.
故答案是:3
-4;10.
∴∠CC1B=∠C1CB=60°,
∴∠CC1A1=∠CC1B+∠A1C1B=60°+60°=120°.

(2)∵△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴
| BA |
| BC |
| BA1 |
| BC1 |
∴∠ABA1=∠CBC1,
∴△ABA1∽△CBC1.
∴
| A△ABA1 |
| S△CBC1 |
| AB |
| BC |
| 8 |
| 6 |
| 16 |
| 9 |

∵S△ABA1=12,
∴S△CBC1=
| 27 |
| 4 |
(3)①如图1,过点B作BD⊥AC,D为垂足,
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin60°=6×
| ||
| 2 |
| 3 |
当P在AC上运动,BP与AC垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1-BE=BD-BE=3
| 3 |
②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BC+BE=6+4=10.
故答案是:3
| 3 |
点评:此题考查了旋转的性质、相似三角形的判定与性质、全等三角形的判定与性质以及三角函数的应用.此题难度较大,注意数形结合思想的应用,注意旋转前后的对应关系.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
点(-2,a)关于原点对称后的坐标为(b,3),a+b的值为( )
| A、1 | B、5 | C、-1 | D、-5 |
计算:6
×
÷2
的结果是( )
| 7 |
| 1 |
| 3 |
| 21 |
| 3 |
| A、-4 | ||
B、-2
| ||
| C、40 | ||
| D、7 |

 某市出租车管理处公示的出租车运价如图:
某市出租车管理处公示的出租车运价如图: (1)如图1,两个相同的正方形重叠摆放,若在图形中随机取点(不包括边线),则点取在阴影部分的概率是
(1)如图1,两个相同的正方形重叠摆放,若在图形中随机取点(不包括边线),则点取在阴影部分的概率是