题目内容
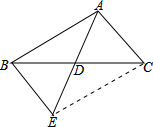
 如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
考点:中心对称
专题:
分析:(1)直接利用中心对称的定义写出答案即可;
(2)根据成中心对称的图形的两个图形全等确定三角形BDE的面积,根据等底同高确定ABD的面积,从而确定ABE的面积;
(3)可证△ABD≌△CDE,可得AB=CE,AD=DE,在△ACE中,根据三角形三边关系即可求得AE的取值范围,即可解题.
(2)根据成中心对称的图形的两个图形全等确定三角形BDE的面积,根据等底同高确定ABD的面积,从而确定ABE的面积;
(3)可证△ABD≌△CDE,可得AB=CE,AD=DE,在△ACE中,根据三角形三边关系即可求得AE的取值范围,即可解题.
解答:解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;
(3)∵在△ABD和△CDE中,
,
∴△ABD≌△CDE(SAS),
∴AB=CE,AD=DE
∵△ACE中,AC-AB<AE<AC+AB,
∴2<AE<8,
∴2<AD<8.
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;

(3)∵在△ABD和△CDE中,
|
∴△ABD≌△CDE(SAS),
∴AB=CE,AD=DE
∵△ACE中,AC-AB<AE<AC+AB,
∴2<AE<8,
∴2<AD<8.
点评:本题考查了中心对称的定义,解题的关键是了解中心对称的定义,难度较小.(3)题考查了全等三角形的判定与性质,本题中求证△ABD≌△CDE是解题的关键.

练习册系列答案
相关题目
下列图形中,对称轴最多的是( )
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
如果n边形的内角和等于外角和的3倍,那么n的值是( )
| A、5 | B、6 | C、7 | D、8 |
 在Rt△ABC中,∠C=90°,b=5,c=5
在Rt△ABC中,∠C=90°,b=5,c=5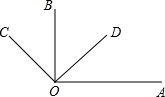 如图,OA⊥OB,OC⊥OD,若∠AOC=135°,则∠BOD=
如图,OA⊥OB,OC⊥OD,若∠AOC=135°,则∠BOD= 如图,点F,E分别是AB,AC上的点,连接FE交BC的延长线于点D,AE•CE=EF•ED.找出图中所有相似的三角形,并证明.
如图,点F,E分别是AB,AC上的点,连接FE交BC的延长线于点D,AE•CE=EF•ED.找出图中所有相似的三角形,并证明.